第四章 多变量线性回归(Linear Regression with Multiple Variables)

Multiple Features（多维特征）

在这段视频中 我们将开始 介绍一种新的 更为有效的线性回归形式 这种形式适用于多个变量或者多特征量的情况

• 在之前我们学习过的 线性回归中 我们只有一个单一特征量 房屋面积 x 我们希望用这个特征量 来预测 房子的价格 这就是我们的假设

• 但是想象一下 如果我们不仅有房屋面积 作为预测房屋 价格的特征量 或者变量 我们还知道 卧室的数量 楼层的数量以及房子的使用年限 这样就给了我们 更多可以用来 预测房屋价格的信息

• 先简单介绍一下记法 我们开始的时候就提到过 我要用 x 下标1 x 下标2 等等 来表示 这种情况下的四个特征量 然后仍然用 Y来表示我们 所想要预测的输出变量

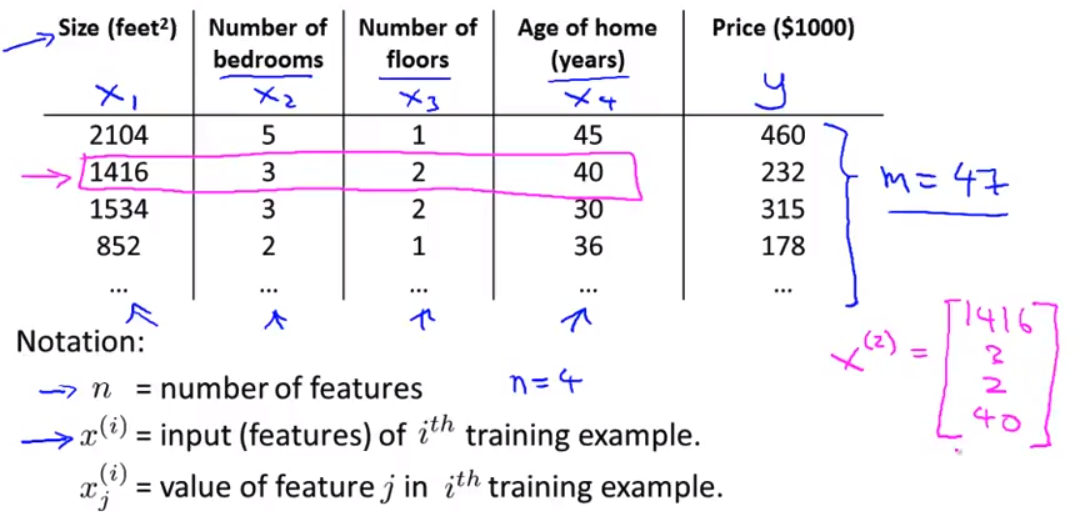
• 让我们来看看更多的表示方式 现在我们有四个特征量 我要用小写n 来表示特征量的数目 因此在这个例子中 我们的n等于4 因为你们看 我们有 1 2 3 4 共4个特征量 这里的n和我们之前 使用的n不同 之前我们是用的“m”来表示样本的数量 所以如果你有47行 那么m就是这个表格里面的行数 或者说是训练样本数

• 然后我要用x 上标 (i) 来表示第i个 训练样本的 输入特征值 举个具体的例子来说 x上标 (2) 就是表示第二个 训练样本的特征向量 因此这里 x(2)就是向量 [1416, 3, 2, 40] 因为这四个数字对应了 我用来预测房屋价格的 第二个房子的 四个特征量 因此在这种记法中 这个上标2 就是训练集的一个索引 而不是x的2次方 这个2就对应着 你所看到的表格中的第二行 即我的第二个训练样本

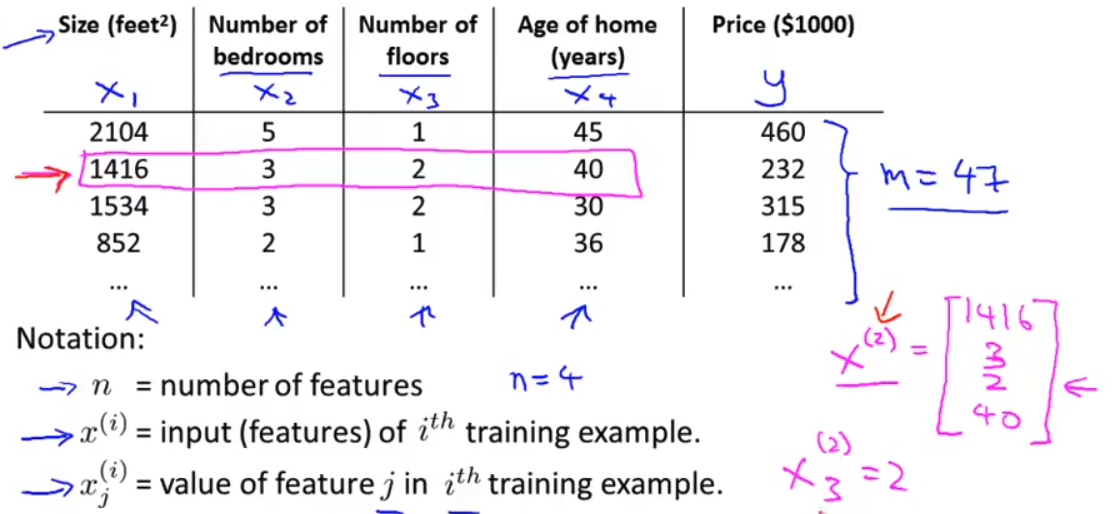
• x上标(2) 这样表示 就是一个四维向量 事实上更普遍地来说 这是n维的向量 用这种表示方法 x上标2就是一个向量 因此 我用x上标(i) 下标j 来表示 第i个训练样本的 第j个特征量 因此具体的来说 x上标(2)下标3代表着 第2个训练样本里的第3个特征量 对吧？ 这个是3 我写的不太好看 所以说x上标(2)下标3就等于2

• 既然我们有了多个特征量 让我们继续讨论一下 我们的假设形式应该是怎样的 这是我们之前使用的假设形式 x就是我们唯一的特征量 但现在我们有了多个特征量 我们就不能再 使用这种简单的表示方式了 取而代之的 我们将把线性回归的假设 改成这样 θ0加上 θ1 乘以 x1 加上 θ2乘以x2 加上 θ3 乘以x3 加上θ4乘以x4 然后如果我们有n个特征量 那么我们要将所有的n个特征量相加 而不是四个特征量 我们需要对n个特征量进行相加

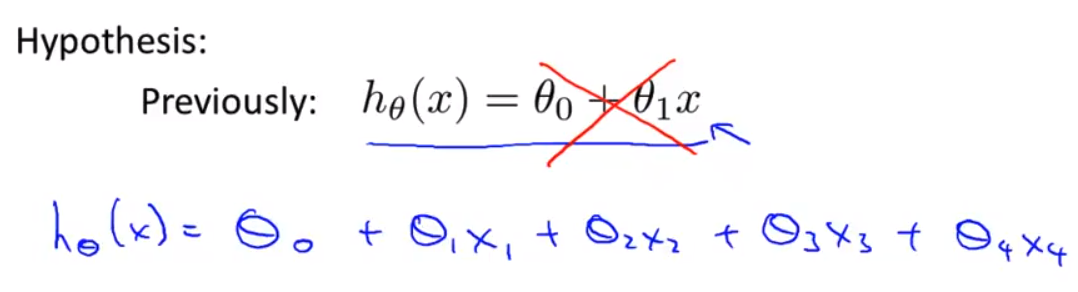
• 举个具体的例子 在我们的设置的参数中 我们可能有h(x)等于 80 + 0.1 x1 + 0.01x2 + 3x3 - 2x4 这就是一个 假设的范例 别忘了 假设是为了预测 大约以千刀为单位的房屋价格 就是说 一个房子的价格 可以是 80 k加上 0.1乘以x1 也就是说 每平方尺100美元 然后价格 会随着楼层数的增加 再继续增长 x2是楼层数 接着价格会继续增加 随着卧室数的增加 因为x3是 卧室的数量 但是呢 房子的价格会 随着使用年数的增加 而贬值

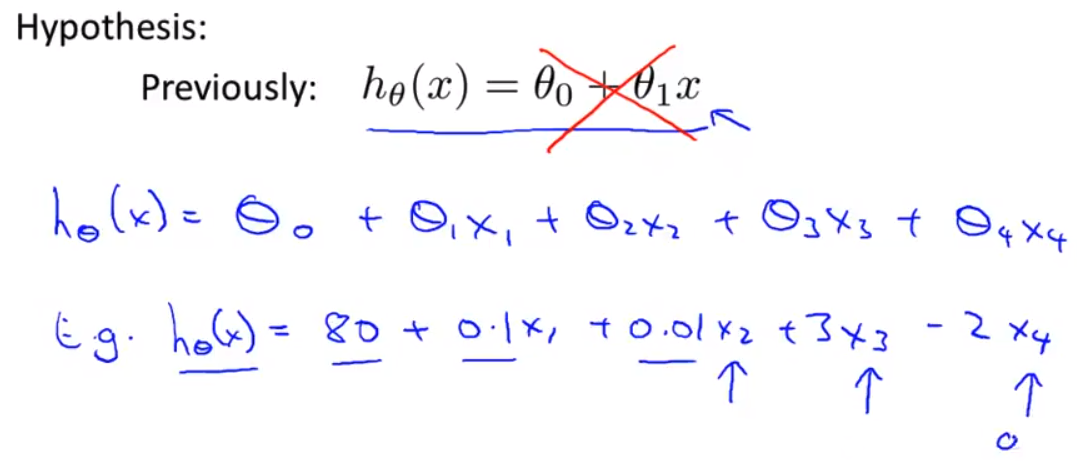
• 这是重新改写过的假设的形式 接下来 我要来介绍一点 简化这个等式的表示方式

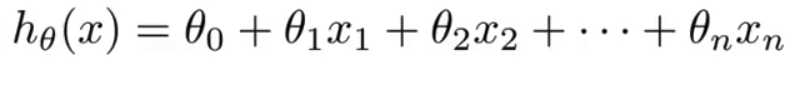
• 为了表示方便 我要将x下标0的值设为1

• 具体而言 这意味着 对于第i个样本 都有一个向量x上标(i) 并且x上标(i) 下标0等于1 你可以认为我们 定义了一个额外的第0个特征量 因此 我过去有n个特征量 因为我们有x1 x2 直到xn 由于我另外定义了 额外的第0个特征向量 并且它的取值 总是1 所以我现在的特征向量x 是一个从0开始标记的 n+1维的向量

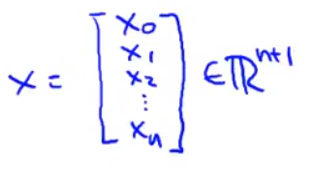
• 所以现在就是一个 n+1维的特征量向量 但我要从0开始标记 同时 我也想把我的参数 都看做一个向量 所以我们的参数就是 我们的θ0 θ1 θ2 等等 直到θn 我们要把 所有的参数都写成一个向量 θ0 θ1...一直到 直到θn 这里也有一个从0开始标记的矢量 下标从0开始 这是另外一个

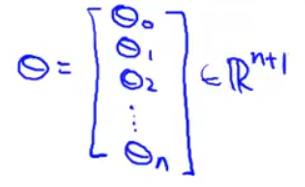
• 所以我的假设 现在可以写成θ0乘以x0 加上θ1乘以x1直到 θn 乘以xn 这个等式 和上面的等式是一样的 因为你看 x0等于1

• 下面 我要 把这种形式假设等式 写成 θ转置乘以X 取决于你对 向量内积有多熟悉 如果你展开 θ转置乘以X 那么就得到 θ0 θ1直到θn 这个就是θ转置 实际上 这就是一个 n+1乘以1维的矩阵 也被称为行向量 用行向量 与X向量相乘 X向量是 x0 x1等等 直到xn 因此内积就是 θ转置乘以X 就等于这个等式

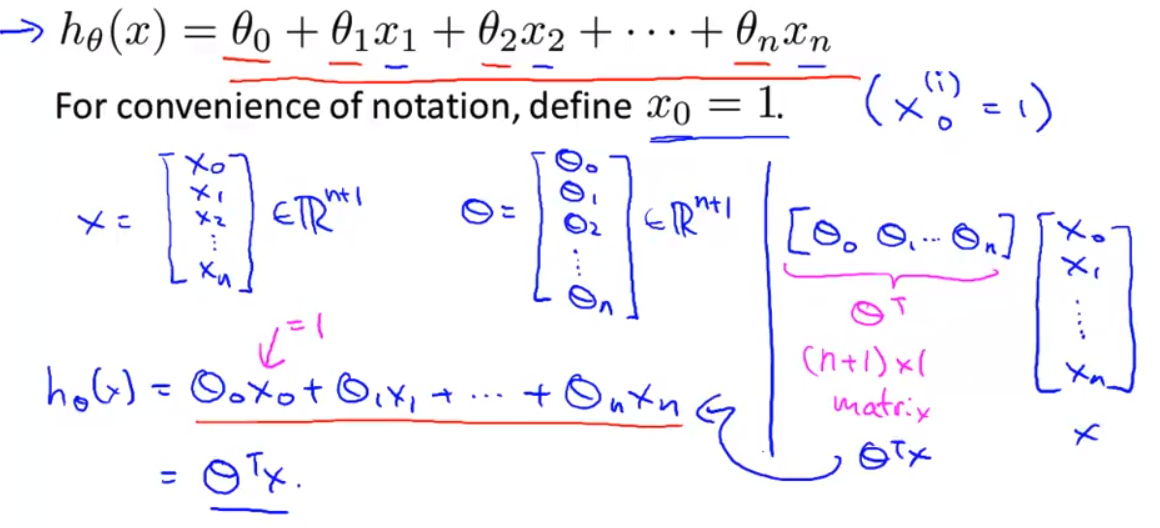
• 这就为我们提供了一个 表示假设的 更加便利的形式 即用参数向量θ以及 特征向量X的内积 这就是改写以后的 表示方法 这样的表示习惯 就让我们 可以以这种紧凑的形式写出假设 这就是多特征量情况下的假设形式 起另一个名字 就是 所谓的多元线性回归
• 多元一词 也就是用来预测的多个特征量 或者变量 就是一种更加好听的说法罢了

Gradient Descent for Multiple Variables(多变量梯度下降)

在之前的视频中 我们谈到了一种线性回归的假设形式 这是一种有多特征或者是多变量的形式 在本节视频中 我们将会谈到如何找到满足这一假设的参数 尤其是如何使用梯度下降法 来解决多特征的线性回归问题

• 为尽快让你理解 现假设现有多元线性回归 并约定 x0=1 该模型的参数是从 θ0 到 θn 不要认为这是 n+1 个单独的参数 你可以把这 n+1 个 θ 参数想象成一个 n+1 维的向量 θ 所以 你现在就可以把这个模型的参数 想象成其本身就是一个n+1 维的向量 我们的代价函数是从 θ0 到 θn 的函数 J 并给出了误差项平方的和 但同样地 不要把函数 J 想成是一个关于 n+1 个自变量的函数 而是看成带有一个 n+1 维向量的函数

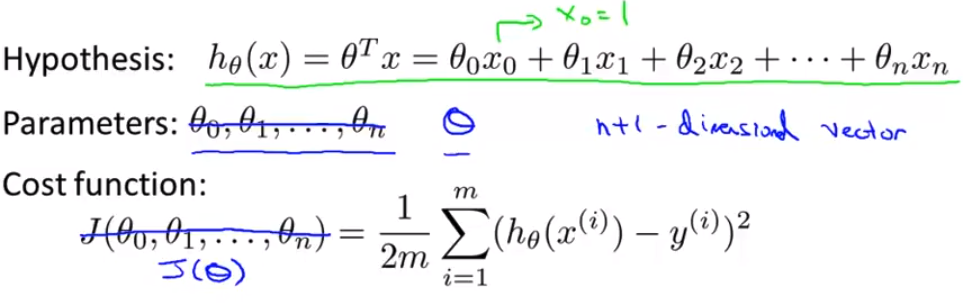
• 这就是梯度下降法 我们将会不停地用 θj 减去 α 倍的导数项 来替代 θj 同样的方法 我们写出函数J(θ) 因此 θj 被更新成 θj 减去学习率 α 与对应导数的乘积 就是代价函数的对参数 θj 的偏导数 当我们实现梯度下降法后 你可以仔细观察一下 尤其是它的偏导数项

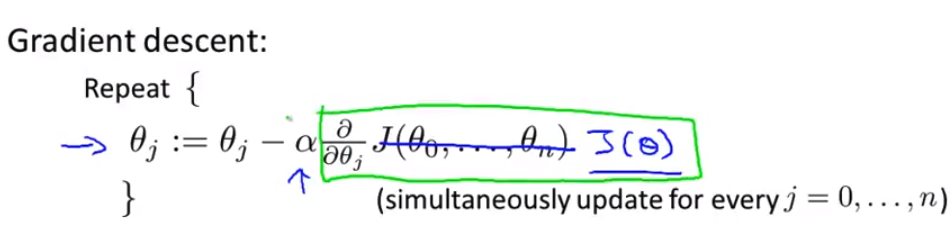
• 下面是我们当特征 n=1 时 梯度下降的情况 我们有两条针对参数 θ0 和 θ1 不同的更新规则 希望这些对你来说并不陌生 这一项是代价函数里部分求导的结果 就是代价函数相对于 θ0 的偏导数

• 同样 对参数 θ1 我们有另一个更新规则 仅有的一点区别是 当我们之前只有一个特征 我们称该特征为x(i) 但现在我们在新符号里 我们会标记它为 x 上标 (i) 下标1 来表示我们的特征 以上就是当我们仅有一个特征时候的算法

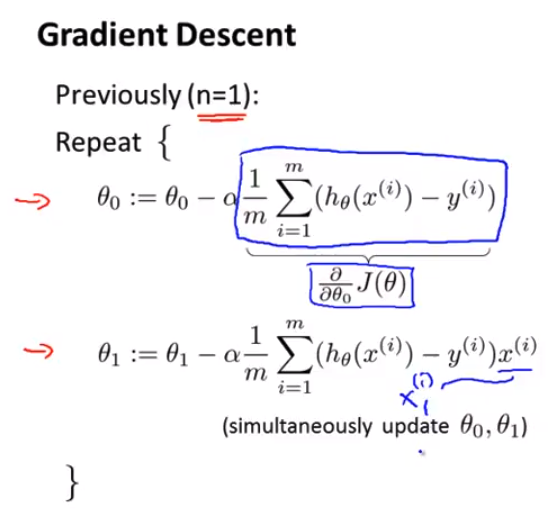
• 下面我们来讲讲当有一个以上特征时候的算法 现有数目远大于1的很多特征 我们的梯度下降更新规则变成了这样 有些同学可能知道微积分 如果你看看代价函数 代价函数 J 对参数 θj 求偏导数 你会发现 求其偏导数的那一项 我已经用蓝线圈出来了 如果你实现了这一步 你将会得到多元线性回归的梯度下降算法

• 最后 我想让你明白 为什么新旧两种算法实际上是一回事儿 或者说为什么这两个是类似的算法 为什么它们都是梯度下降算法 考虑这样一个情况 有两个或以上个数的特征 同时我们有对θ1、θ2、θ3的三条更新规则 当然可能还有其它参数 如果你观察θ0的更新规则 你会发现这跟之前 n=1的情况相同 它们之所以是等价的 这是因为在我们的标记约定里有 x(i)0=1 也就是 我用品红色圈起来的两项是等价的 同样地 如果你观察 θ1 的更新规则 你会发现这里的这一项是 和之前对参数θ1的更新项是等价的

• 在这里我们只是用了新的符号x(i)1来表示我们的第一个特征 现在我们有个更多的特征 那么就可以用与之前相同的更新规则 我们可以用同样的规则来处理 θ2 等其它参数 这张幻灯片的内容不少 请务必仔细理解 如果觉得幻灯片上数学公式没看懂 尽管暂停视频 请确保理解了再继续后面的学习 如果你将这些算法都实现了 那么你就可以直接应用到多元线性回归中了

多变量梯度下降笔记

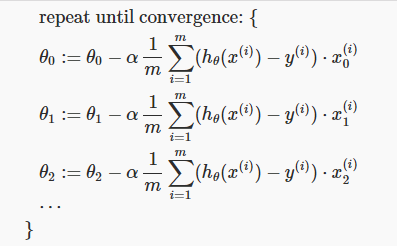
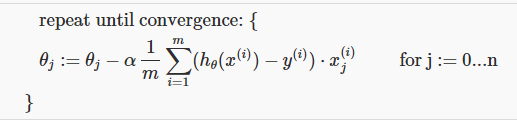
Gradient Descent in Practice 1-Feature Sacling(梯度下降法实践1-特征缩放)

在这段视频 以及下一段视频中 我想告诉你一些关于 梯度下降运算中的实用技巧 在这段视频中 我会告诉你一个称为特征缩放 (feature scaling) 的方法

• 如果你有一个机器学习问题 这个问题有多个特征 如果你能确保这些特征 都处在一个相近的范围 我的意思是确保不同特征的取值 在相近的范围内,这样梯度下降法就能更快地收敛
• 具体地说 假如你有一个具有两个特征的问题 其中 x1 是房屋面积大小 它的取值 在0到2000之间 x2 是卧室的数量 可能这个值 取值范围在1到5之间 如果你画出代价函数 J(θ) 的轮廓图 那么这个轮廓看起来 应该是像这样的 J(θ) 是一个关于 参数 θ0 θ1 和 θ2 的函数 但我要忽略 θ0 所以暂时不考虑 θ0 并假想一个函数的变量 只有 θ1 和 θ2 但如果 x1 的取值范围 远远大于 x2 的取值范围的话 那么最终画出来的 代价函数 J(θ) 的轮廓图 就会呈现出这样一种 非常偏斜 并且椭圆的形状 2000 和 5的比例 会让这个椭圆更加瘦长 所以 这是一个又瘦又高的 椭圆形轮廓图 就是这些非常高大细长的椭圆形 构成了代价函数 J(θ)

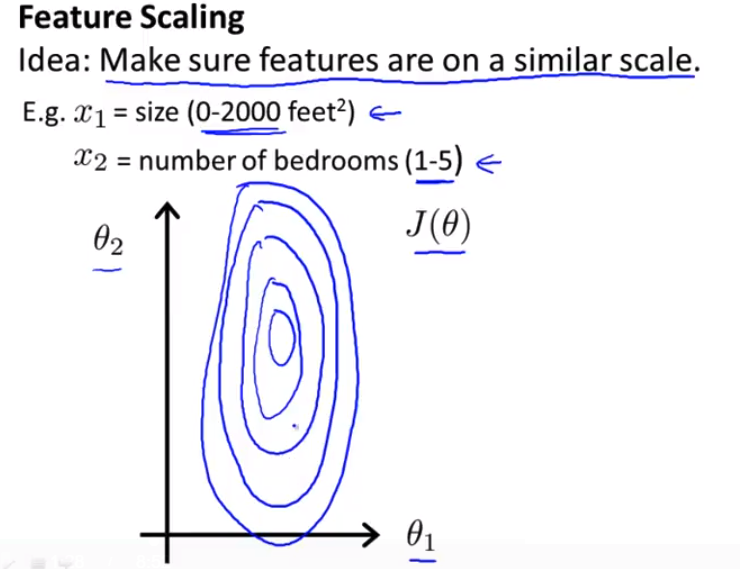
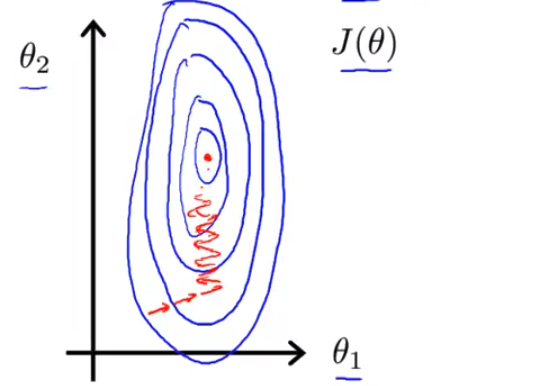
• 而如果你用这个代价函数 来运行梯度下降的话 你要得到梯度值 最终可能 需要花很长一段时间 并且可能会来回波动 然后会经过很长时间 最终才收敛到全局最小值

• 事实上 你可以想像 如果这些 轮廓再被放大一些的话 如果你画的再夸张一些 把它画的更细更长 那么可能情况会更糟糕 梯度下降的过程 可能更加缓慢 需要花更长的时间 反复来回振荡 最终才找到一条正确通往全局最小值的路

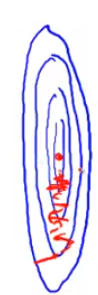
• 在这样的情况下 一种有效的方法是进行特征缩放(feature scaling) 具体来说 把特征 x 定义为 房子的面积大小 除以2000的话 并且把 x2 定义为 卧室的数量除以5 那么这样的话 表示代价函数 J(θ) 的轮廓图的形状 就会变得偏移没那么严重 可能看起来更圆一些了

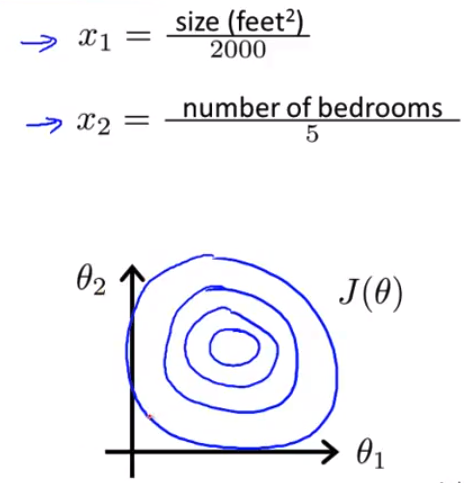
• 如果你用这样的代价函数 来执行梯度下降的话 那么 梯度下降算法

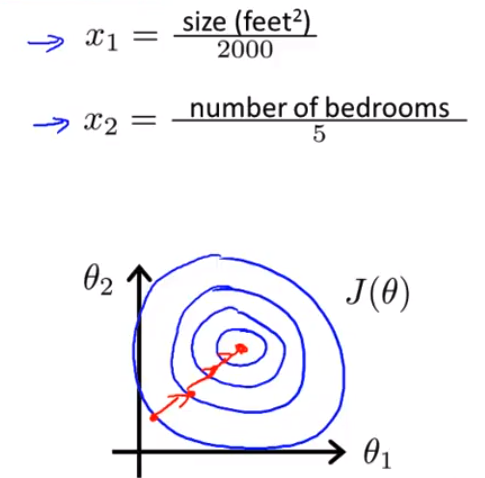
• 你可以从数学上来证明 梯度下降算法 就会找到一条 更捷径的路径通向全局最小 而不是像刚才那样 沿着一条让人摸不着头脑的路径 一条复杂得多的轨迹 来找到全局最小值 因此 通过特征缩放 通过”消耗掉”这些值的范围 在这个例子中 我们最终得到的两个特征 x1 和 x2 都在0和1之间 这样你得到的梯度下降算法 就会更快地收敛
• 更一般地 我们执行特征缩放时 我们通常的目的是 将特征的取值约束到 -1 到 +1 的范围内 你的特征 x0 是总是等于1 因此 这已经是在这个范围内 但对其他的特征 你可能需要通过除以不同的数 来让它们处于同一范围内

• -1 和 +1 这两个数字并不是太重要 所以 如果你有一个特征 x1 它的取值 在0和3之间 这没问题 如果你有另外一个特征 取值在-2 到 +0.5之间 这也没什么关系 这也非常接近 -1 到 +1的范围 这些都可以

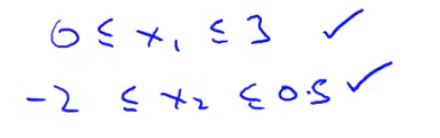
• 但如果你有另一个特征 比如叫 x3 假如它的范围 在 -100 到 +100之间 那么 这个范围 跟-1到+1就有很大不同了 所以 这可能是一个 不那么好的特征 类似地 如果你的特征在一个 非常非常小的范围内 比如另外一个特征 x4 它的范围在 0.0001和+0.0001之间 那么 这同样是一个 比-1到+1小得多的范围 比-1到+1小得多的范围 因此 我同样会认为这个特征也不太好

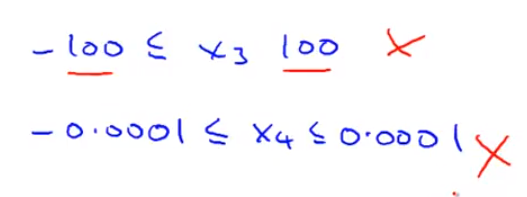
• 所以 可能你认可的范围 也许可以大于 或者小于 -1 到 +1 但是也别太大 只要大得不多就可以接受 比如 +100 或者也别太小 比如这里的0.001 不同的人有不同的经验 但是我一般是这么考虑的 如果一个特征是在 -3 到 +3 的范围内 那么你应该认为 这个范围是可以接受的 但如果这个范围 大于了 -3 到 +3 的范围 我可能就要开始注意了 如果它的取值 在-1/3 到+1/3的话 我觉得 还不错 可以接受 或者是0到1/3 或-1/3到0 这些典型的范围 我都认为是可以接受的 但如果特征的范围 取得很小的话 比如像这里的 x4 你就要开始考虑进行特征缩放了
• 因此 总的来说 不用过于担心 你的特征是否在完全 相同的范围或区间内 但是只要他们都 只要它们足够接近的话 梯度下降法就会正常地工作
• 除了在特征缩放中 将特征除以最大值以外 有时候我们也会进行一个 称为均值归一化的工作(mean normalization) 我的意思是这样的 如果你有一个特征 xi 你就用 xi - μi 来替换 通过这样做 让你的特征值 具有为0的平均值 很明显 我们不需要 把这一步应用到 x0中 因为 x0 总是等于1的 所以它不可能有 为0的的平均值
• 但是 对其他的特征来说 比如房子的大小 取值介于0到2000 并且假如 房子面积 的平均值 是等于1000的 那么你可以用这个公式 将 x1 的值变为 x1 减去平均值 μ1 再除以2000 类似地 如果你的房子有 五间卧室 并且平均一套房子有 两间卧室 那么你可以 使用这个公式 来归一化你的第二个特征 x2 在这两种情况下 你可以算出新的特征 x1 和 x2 这样它们的范围 可以在-0.5和+0.5之间 当然这肯定不对 x2的值实际上肯定会大于0.5 但很接近

• 更一般的规律是 你可以用这样的公式 你可以用 (x1 - μ1)/S1 来替换原来的特征 x1 其中定义μ1的意思是 在训练集中 特征 x1 的平均值 而 S1 是 该特征值的范围 我说的范围是指 最大值减去最小值或者学过 标准差的同学可以记住 也可以把 S1 设为 变量的标准差 但其实用最大值减最小值就可以了 类似地 对于第二个 特征 x2 你也可以用同样的这个 特征减去平均值 再除以范围 来替换原特征 范围的意思依然是最大值减最小值 这类公式将 把你的特征 变成这样的范围 也许不是完全这样 但大概是这样的范围

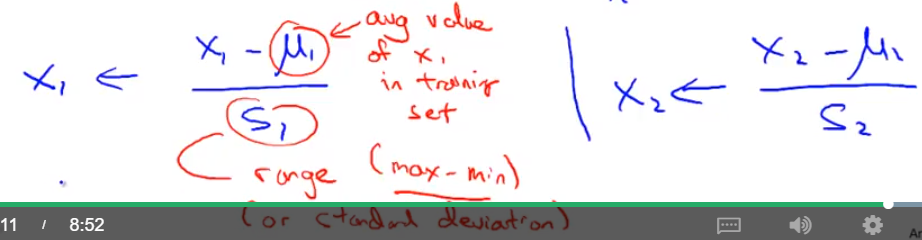
• 顺便提一下 有些同学可能比较仔细 如果我们用最大值减最小值 来表示范围的话 这里的5有可能应该是4 如果最大值为5 那么减去最小值1 这个范围值就是4 但不管咋说 这些取值 都是非常近似的 只要将特征转换为 相近似的范围 就都是可以的 特征缩放其实 并不需要太精确 只是为了让梯度下降 能够运行得更快一点而已
• 好的 现在你知道了 什么是特征缩放 通过使用这个简单的方法 你可以将梯度下降的速度变得更快 让梯度下降收敛所需的循环次数更少 这就是特征缩放 在接下来的视频中 我将介绍另一种技巧来使梯度下降 在实践中工作地更好

Gradient Descent in Practice II-Learning Rate(梯度下降法实践2-学习率)

在本段视频中 我想告诉大家 一些关于梯度下降算法的实用技巧 我将集中讨论 学习率 α 具体来说 这是梯度下降算法的 更新规则 这里我想要 告诉大家 如何调试 也就是我认为应该如何确定 梯度下降是正常工作的 此外我还想告诉大家 如何选择学习率 α 也就是我平常 如何选择这个参数 我通常是怎样确定 梯度下降正常工作的

• 梯度下降算法所做的事情 就是为你找到 一个 θ 值 并希望它能够最小化代价函数 J(θ) *我通常会在 梯度下降算法运行时 绘出代价函数 J(θ) 的值 这里的 x 轴是表示 *梯度下降算法的 迭代步数 你可能会得到 这样一条曲线 注意 这里的 x 轴 是迭代步数 在我们以前看到的 J(θ) 曲线中 x 轴 也就是横轴 曾经用来表示参数 θ 但这里不是 具体来说 这一点的含义是这样的 当我运行完100步的梯度下降迭代之后 无论我得到 什么 θ 值 总之 100步迭代之后 我将得到 一个 θ 值 根据100步迭代之后 得到的这个 θ 值 我将算出 代价函数 J(θ) 的值 而这个点的垂直高度就代表 梯度下降算法 100步迭代之后 得到的 θ 算出的 J(θ) 值

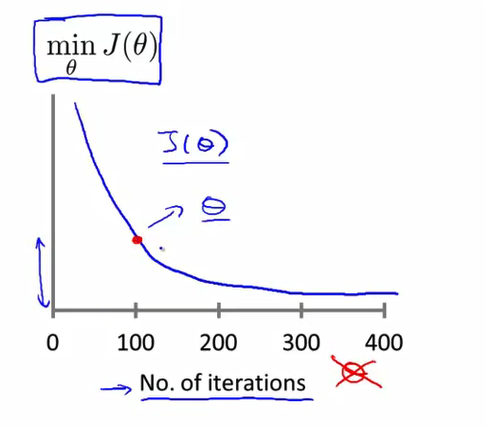
• 而这个点 则是梯度下降算法 迭代200次之后 得到的 θ 算出的 J(θ) 值 所以这条曲线 显示的是 梯度下降算法迭代过程中代价函数 J(θ) 的值 如果梯度下降算法 正常工作 那么每一步迭代之后 J(θ) 都应该下降 这条曲线 的一个用处在于 它可以告诉你 如果你看一下 我画的这条曲线 当你达到 300步迭代之后 也就是300步到400步迭代之间 就是曲线的这一段 看起来 J(θ) 并没有下降多少 所以当你 到达400步迭代时 这条曲线看起来已经很平坦了 也就是说 在这里400步迭代的时候 梯度下降算法 基本上已经收敛了 因为代价函数并没有继续下降 所以说 看这条曲线 可以帮助你判断 梯度下降算法是否已经收敛

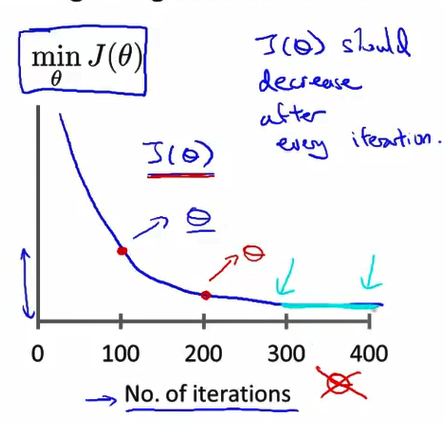
• 顺便说一下 对于每一个特定的问题 梯度下降算法所需的迭代次数 可以相差很大 也许对于某一个问题 梯度下降算法 只需要30步迭代就可以收敛 然而换一个问题 也许梯度下降算法就需要3000步迭代 对于另一个机器学习问题 则可能需要三百万步迭代 实际上 我们很难提前判断
• 梯度下降算法 需要多少步迭代才能收敛 通常我们需要画出这类曲线 画出代价函数随迭代步数数增加的变化曲线 通常 我会通过看这种曲线 来试着判断 梯度下降算法是否已经收敛 另外 也可以 进行一些自动的收敛测试 也就是说用一种算法 来告诉你梯度下降算法 是否已经收敛 自动收敛测试 一个非常典型的例子是 如果代价函数 J(θ) 的下降小于 一个很小的值 ε 那么就认为已经收敛 比如可以选择 1e-3 但我发现 通常要选择一个合适的阈值 ε 是相当困难的 因此 为了检查 梯度下降算法是否收敛 我实际上还是 通过看 左边的这条曲线图 而不是依靠自动收敛测试

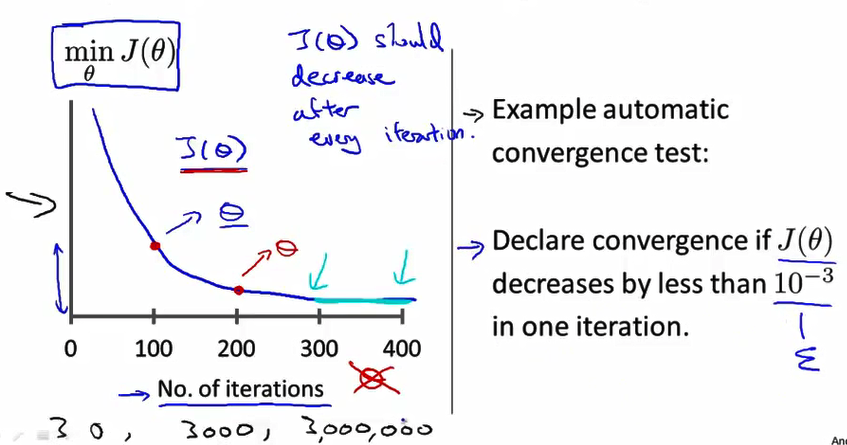
• 此外 这种曲线图 也可以 在算法没有正常工作时 提前警告你 具体地说 如果代价函数 J(θ) 随迭代步数 的变化曲线是这个样子 J(θ) 实际上在不断上升 那就很明显的表示 梯度下降算法没有正常工作 而这样的曲线,通常意味着你应该使用较小的学习率a

• 这样的曲线图表示你的学习率a太大了,因此得到的结果也会不断跳过最小值,变得越来越大,因此应该使用较小的学习率a

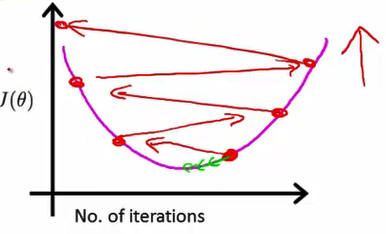
• 这种图也是要选择小的a

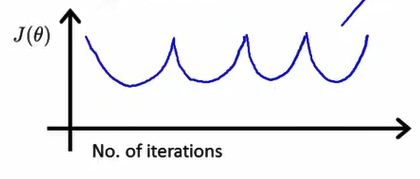
• a不可以太大,也不可以太小

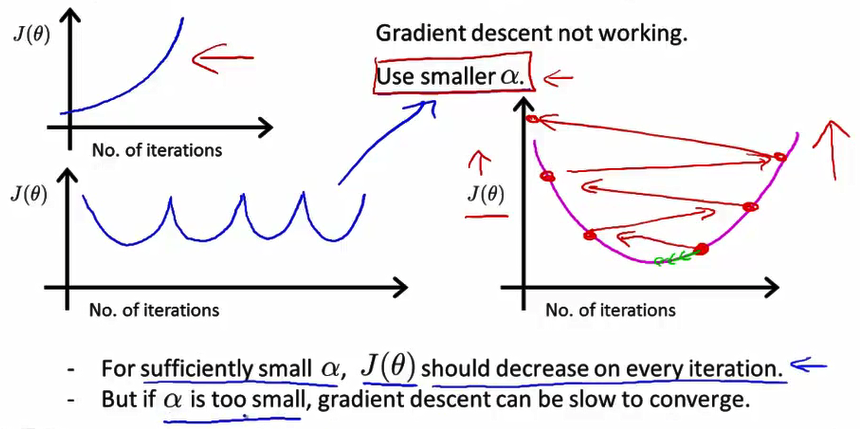
• 一般尝试的a值

Features and Polynomial Regression 特征和多项式回归

你现在了解了多变量的线性回归 在本段视频中 我想告诉你 一些用来 选择特征的方法以及 如何得到不同的学习算法 当选择了合适的特征后 这些算法往往是非常有效的 另外 我也想 给你们讲一讲多项式回归 它使得你们能够使用 线性回归的方法来拟合 非常复杂的函数 甚至是非线性函数

• 以预测房价为例 假设你有两个特征 分别是房子临街的宽度和垂直宽度 这就是我们想要卖出的房子的图片 临街宽度 被定义为这个距离 其实就是它的宽度 或者说是 你拥有的土地的宽度 如果这块地都是你的的话 而这所房子的 纵向深度就是 你的房子的深度 这是正面的宽度 这是深度 我们称之为临街宽度和纵深 你可能会 像这样 建立一个 线性回归模型 其中临街宽度 是你的第一个特征x1 纵深是你的第二个 特征x2

• 但当我们在 运用线性回归时 你不一定非要直接用 给出的 x1 和 x2 作为特征 其实你可以自己创造新的特征 因此 如果我要预测 房子的价格 我真正要需做的 也许是 确定真正能够决定 我房子大小 或者说我土地大小 的因素是什么 因此 我可能会创造一个新的特征 我称之为 x 它是临街宽度与纵深的乘积 这是一个乘法符号 它是临街宽度与纵深的乘积 这得到的就是我拥有的土地的面积 然后 我可以把 假设选择为 使其只使用 一个特征 也就是我的 土地的面积 对吧？

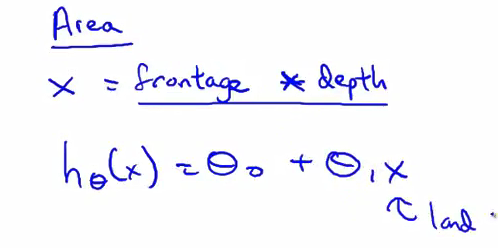
• 由于矩形面积的 计算方法是 矩形长和宽相乘 因此 这取决于 你从什么样的角度 去审视一个特定的问题 而不是 只是直接去使用临街宽度和纵深 这两个我们只是碰巧在开始时 使用的特征 有时 通过定义 新的特征 你确实会得到一个更好的模型
• 与选择特征的想法 密切相关的一个概念 被称为多项式回归(polynomial regression) 比方说 你有这样一个住房价格的数据集 为了拟合它 可能会有多个不同的模型供选择 其中一个你可以选择的是像这样的二次模型 因为直线似乎并不能很好地拟合这些数据 因此 也许你会想到 用这样的二次模型去拟合数据 你可能会考量 是关于价格的一个二次函数 也许这样做 会给你一个 像这样的拟合结果

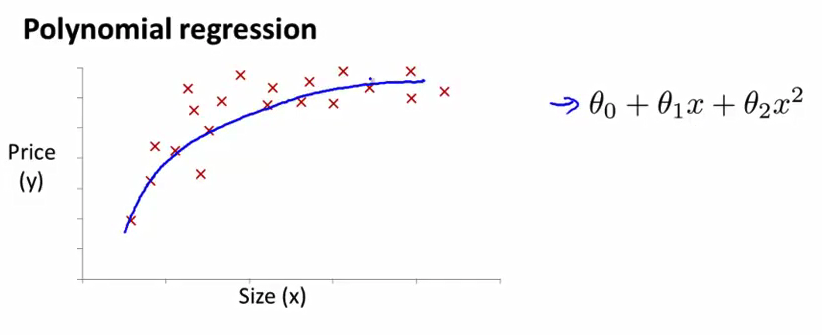
• 但是 然后你可能会觉得 二次函数的模型并不好用 因为 一个二次函数最终 会降回来 而我们并不认为 房子的价格在高到一定程度后 会下降回来

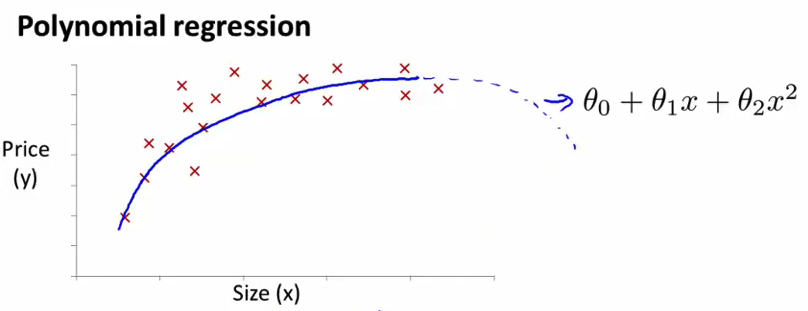
• 因此 也许我们会 选择一个不同的多项式模型 并转而选择使用一个 三次函数 在这里 现在我们有了一个三次的式子 我们用它进行拟合 我们可能得到这样的模型 也许这条绿色的线 对这个数据集拟合得更好 因为它不会在最后下降回来

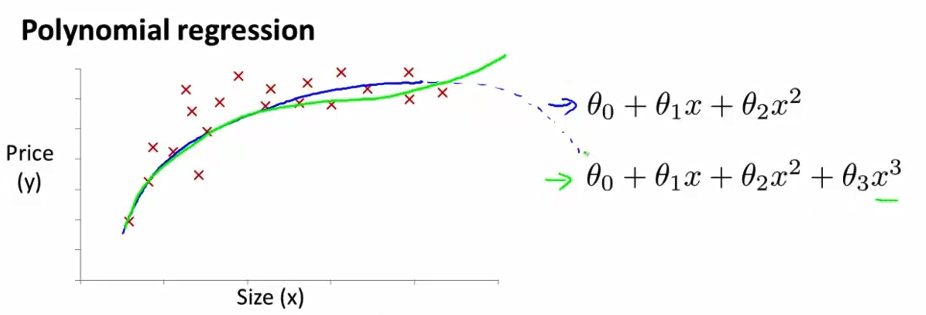
• 那么 我们到底应该如何将模型与我们的数据进行拟合呢？ 使用多元线性回归的方法 我们可以 通过将我们的算法做一个非常简单的修改来实现它 按照我们以前假设的形式 我们知道如何对 这样的模型进行拟合 其中 ħθ(x) 等于 θ0 +θ1×x1 + θ2×x2 + θ3×x3 那么 如果我们想 拟合这个三次模型 就是我用绿色方框框起来的这个 现在我们讨论的是 为了预测一栋房子的价格 我们用 θ0 加 θ1 乘以房子的面积 加上 θ2 乘以房子面积的平方 因此 这个式子与那个式子是相等的 然后再加 θ3 乘以 房子面积的立方 为了将这两个定义 互相对应起来 为了做到这一点 我们自然想到了 将 x1 特征设为 房子的面积 将第二个特征 x2 设为 房屋面积的平方 将第三个特征 x3 设为 房子面积的立方

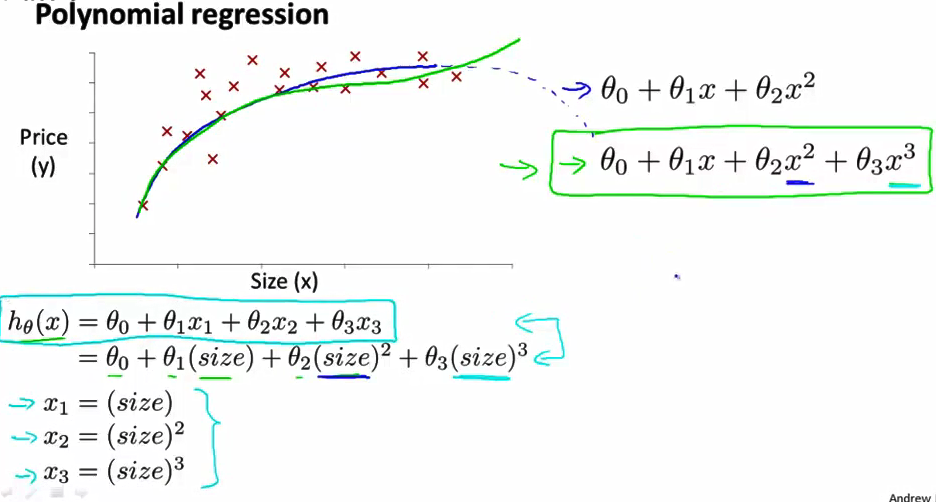
• 那么 仅仅通过将 这三个特征这样设置 然后再应用线性回归的方法 我就可以拟合 这个模型 并最终 将一个三次函数拟合到我的数据上 我还想再说一件事 那就是 如果你像这样选择特征 那么特征的归一化 就变得更重要了 因此 如果 房子的大小范围在 1到1000之间 那么 比如说 从1到1000平方尺 那么 房子面积的平方 的范围就是 一到一百万 也就是 1000的平方 而你的第三个特征 x的立方 抱歉 你的第三个特征 x3 它是房子面积的 立方 范围会扩大到 1到10的9次方 因此 这三个特征的范围 有很大的不同 因此 如果你使用梯度下降法 应用特征值的归一化是非常重要的 这样才能将他们的 值的范围变得具有可比性

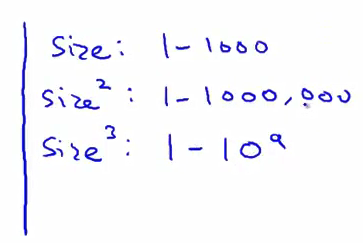
• 最后 这里是最后一个例子 关于如何使你 真正选择出要使用的特征 此前我们谈到 一个像这样的二次模型 并不是理想的 因为 你知道 也许一个二次模型能很好地拟合 这个数据 但二次 函数最后会下降 这是我们不希望的 就是住房价格往下走 像预测的那样 出现房价的下降 但是 除了转而 建立一个三次模型以外 你也许有其他的选择 特征的方法 这里有很多可能的选项 但是给你另外一个 合理的选择的例子

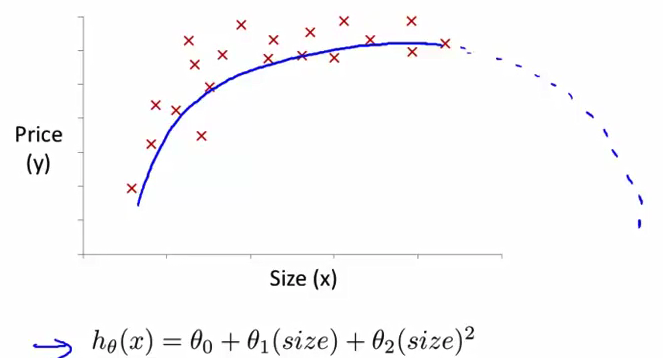
• 另一种合理的选择 可能是这样的 一套房子的价格是 θ0 加 θ1 乘以 房子的面积 然后 加 θ2 乘以房子面积的平方根 可以吧？

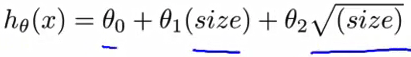
• 平方根函数是 这样的一种函数 也许θ1 θ2 θ3 中会有一些值 会捕捉到这个模型 从而使得这个曲线看起来 是这样的 趋势是上升的 但慢慢变得 平缓一些 而且永远不会 下降回来

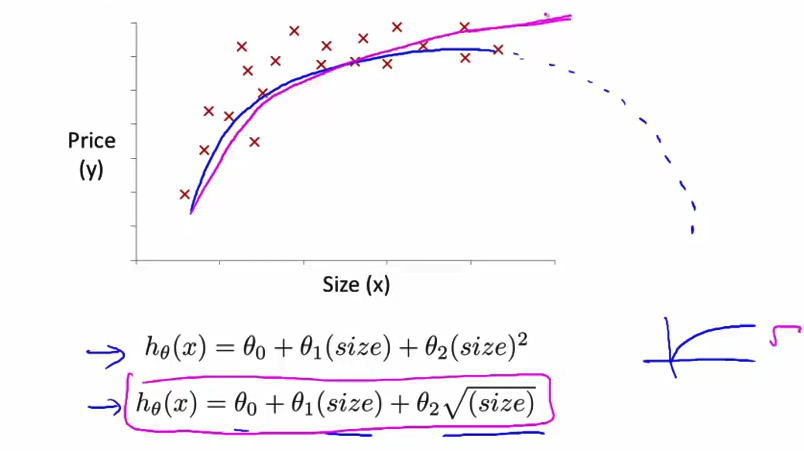
• 因此 通过深入地研究 在这里我们研究了平方根 函数的形状 并且 更深入地了解了选择不同特征时数据的形状 有时可以得到更好的模型 在这段视频中 我们探讨了多项式回归 也就是 如何将一个 多项式 如一个二次函数 或一个三次函数拟合到你的数据上 除了这个方面 我们还讨论了 在使用特征时的选择性 例如 我们不使用 房屋的临街宽度和纵深 也许 你可以 把它们乘在一起 从而得到 房子的土地面积这个特征 实际上 这似乎有点 难以抉择 这里有这么多 不同的特征选择 我该如何决定使用什么特征呢

• 在之后的课程中 我们将 探讨一些算法 它们能够 自动选择要使用什么特征 因此 你可以使用一个算法 观察给出的数据 并自动为你选择 到底应该选择 一个二次函数 或者一个三次函数 还是别的函数 但是 在我们 学到那种算法之前 现在我希望你知道 你需要选择 使用什么特征 并且通过设计不同的特征 你能够用更复杂的函数 去拟合你的数据 而不是只用 一条直线去拟合 特别是 你也可以使用多项式 函数 有时候 通过采取适当的角度来观察 特征就可以 得到一个更符合你的数据的模型

Normal Equation 正规方程

在这段视频中 我们要讲 正规方程 (Normal Equation)对于某些线性回归问题 用正规方程法求解参数 θ 的最优值更好

• 具体而言 到目前为止 我们一直在使用的线性回归的算法 是梯度下降法 就是说 为了最小化代价函数 J(θ) 来最小化这个 我们使用的迭代算法 需要经过很多步 也就是说通过多次迭代来计算梯度下降 来收敛到全局最小值

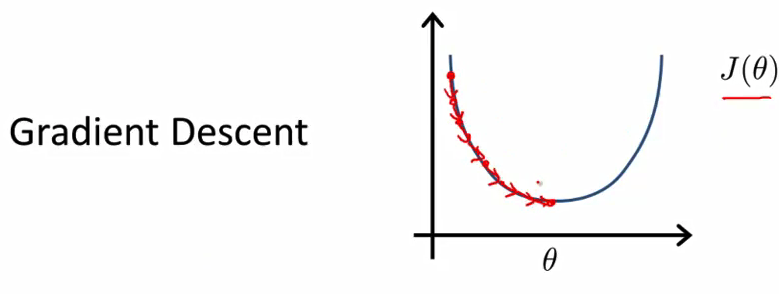
• 相反地 正规方程法提供了一种求 θ 的解析解法 所以与其使用迭代算法 我们可以直接一次性求解θ的最优值 所以说基本上 一步就可以得到优化值

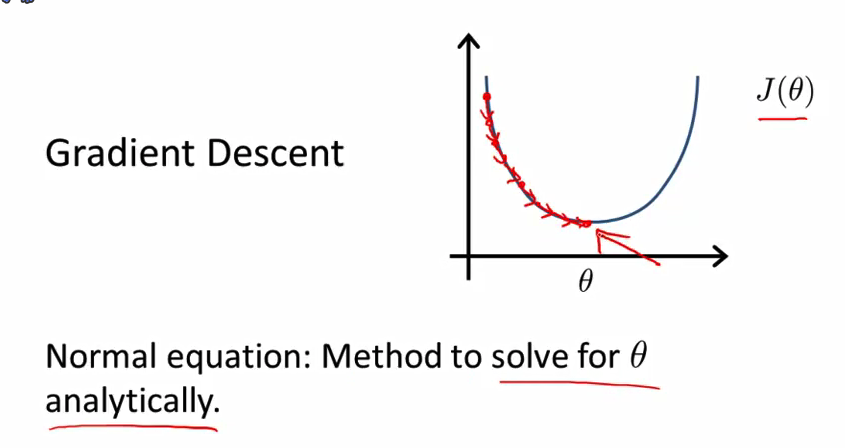
• 正规方程法有一些优点 也有一些缺点 但是在我们讲解这个 和何时使用标准方程之前 让我们先对这个算法有一个直观的理解
• 我们举一个例子来解释这个问题 我们假设 有一个非常简单的代价函数 J(θ) 它就是一个实数 θ 的函数 所以现在 假设 θ 只是一个标量 或者说 θ 只有一行 它是一个数字 不是向量 假设我们的代价函数 J 是这个实参数 θ 的二次函数 所以 J(θ) 看起来是这样的

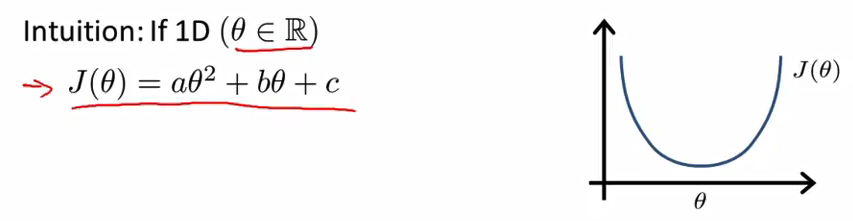
• 那么如何最小化一个二次函数呢? 对于那些了解一点微积分的同学来说 你可能知道 最小化的一个函数的方法是 对它求导 并且将导数置零 所以对 J 求关于 θ 的导数 我不打算推导那些公式 你把那个导数置零 这样你就可以求得 使得 J(θ) 最小的 θ 值 这是数据为实数的 一个比较简单的例子

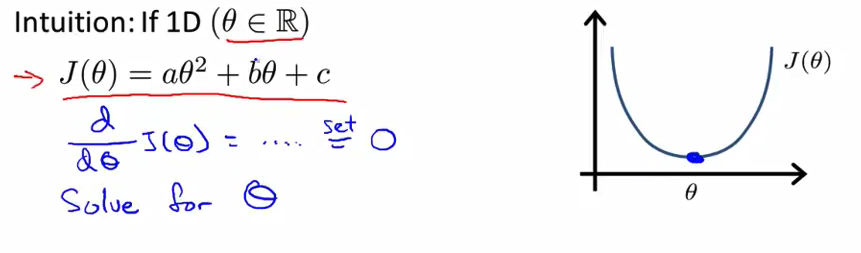
• 在这个问题中 我们感兴趣的是 θ不是一个实数的情况 它是一个n+1维的参数向量 并且 代价函数 J 是这个向量的函数 也就是 θ0 到 θm 的函数 一个代价函数看起来是这样 像右边的这个平方代价函数 我们如何最小化这个代价函数J? 实际上 微积分告诉我们一种方法 对每个参数 θ 求 J 的偏导数 然后把它们全部置零 如果你这样做 并且求出θ0 θ1 一直到θn的值 这样就能得到能够最小化代价函数 J 的 θ 值

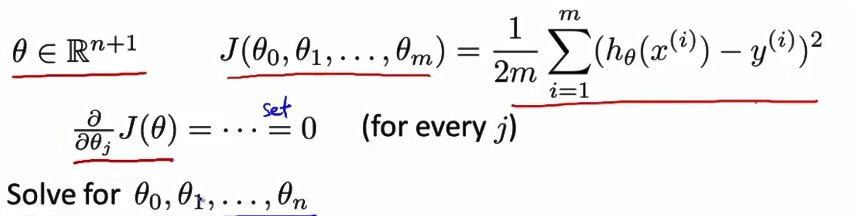
• 如果你真的做完微积分和求解参数 θ0 到 θn 你会发现这个偏微分最终可能很复杂 接下来我在视频中要做的 实际上不是遍历所有的偏微分 因为这样太久太费事 我只是想告诉你们 你们想要实现这个过程所需要知道内容 这样你就可以解出 偏导数为0时 θ的值 换个方式说 或者等价地 这个 θ 能够使得代价函数 J(θ) 最小化 我发现可能只有熟悉微积分的同学 比较容易理解我的话 所以 如果你不了解 或者不那么了解微积分 也不必担心 我会告诉你 要实现这个算法并且使其正常运行 你所需的必要知识

• 举个例子 我想运行这样一个例子 假如说我有 m=4 个训练样本 假如说我有 m=4 个训练样本

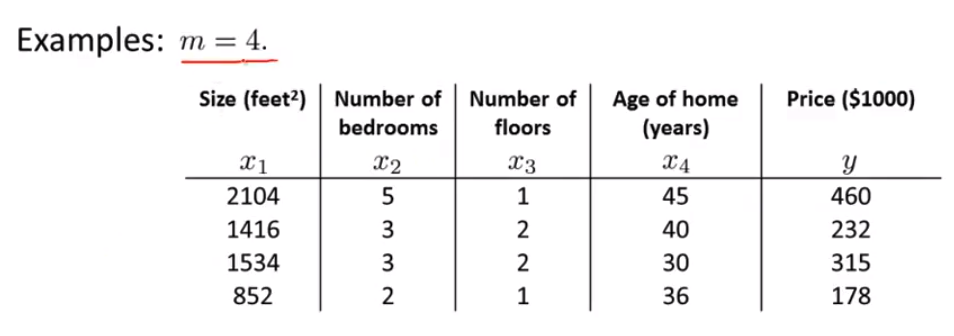
• 为了实现正规方程法 我要这样做 看我的训练集 在这里就是这四个训练样本 在这种情况下 我们假设 这四个训练样本就是我的所有数据 我所要做的是 在我的训练集中加上一列对应额外特征变量的x0 就是那个取值永远是1的

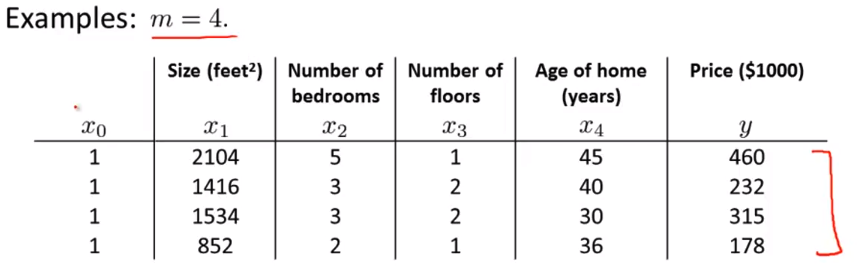
• 接下来我要做的是 构建一个矩阵 X 这个矩阵基本包含了训练样本的所有特征变量 所以具体地说 这里有我所有的特征变量 我们要把这些数字 全部放到矩阵中 X 中 所以只是 每次复制一列的数据

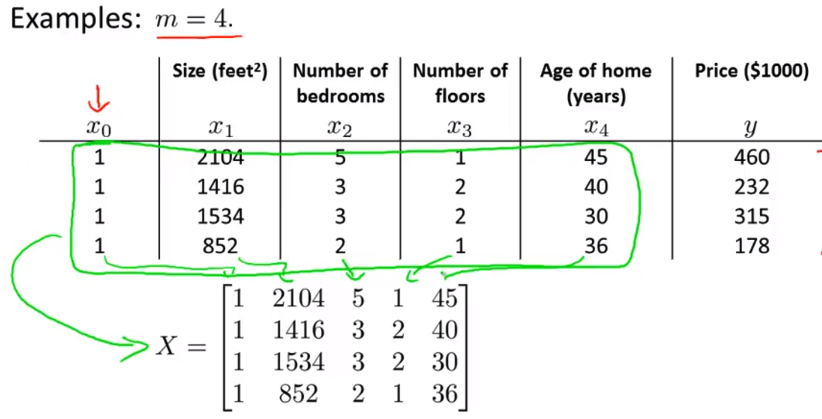
• 我要对 y 做类似的事情 我要对我们将要预测的值 构建一个向量 像这样的 并且称之为向量 y

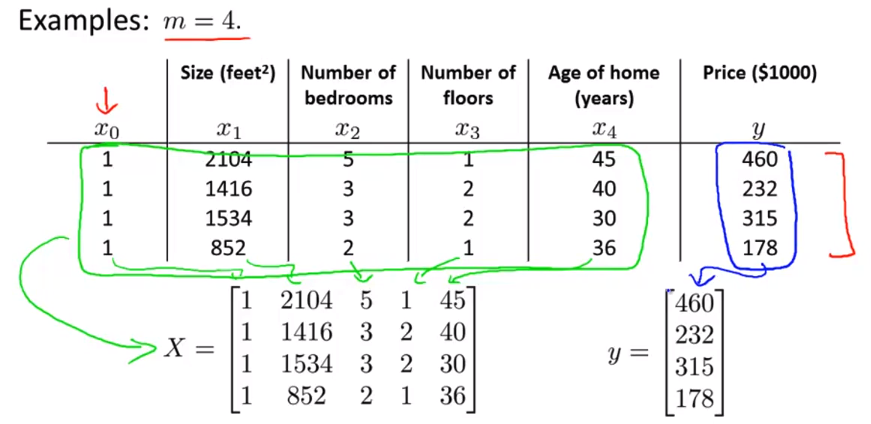
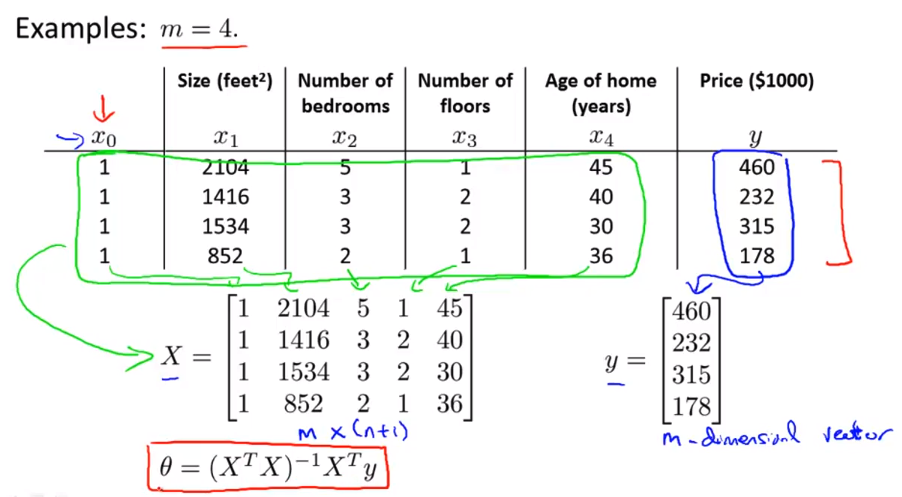
• 所以 X 会是一个 m*(n+1) 维矩阵 y 会是一个 m 维向量 其中 m 是训练样本数量 n 是特征变量数 n+1 是因为我加的这个额外的特征变量 x0 最后 如果你用矩阵 X 和向量 y 来计算这个 最后 θ 等于 X 转置乘以 X 的逆 乘以 X 转置 乘以 y 这样就得到能够使得代价函数最小化的 θ 幻灯片上的内容比较多 我讲解了这样一个数据组的一个例子 让我把这个写成更加通用的形式 在之后的视频中 我会仔细介绍这个方程

• 在一般情况下 假如我们有 m 个训练样本 x(1) y(1) 直到 x(m) y(m) n 个特征变量 所以每一个训练样本 xi 可能看起来像一个向量 像这样一个 n+1 维特征向量

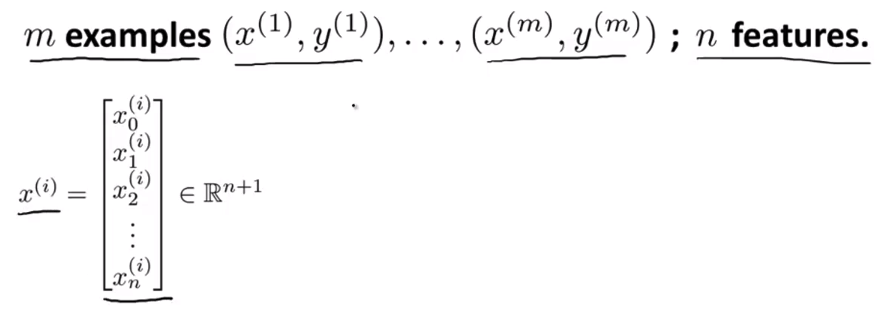
• 我要构建矩阵 X 的方法 也被称为设计矩阵 如下所示 每个训练样本给出一个这样的特征向量 也就是说 这样的 n+1 维向量 我构建我的设计矩阵 X 的方法 就是构建这样的矩阵 接下来我要做的是将 取第一个训练样本 也就是一个向量 取它的转置 它最后是这样 扁长的样子 让 x1 转置作为我设计矩阵的第一行 然后我要把我的 第二个训练样本 x2 进行转置 让它作为 X 的第二行 以此类推 直到最后一个训练样本 取它的转置作为矩阵 X 的最后一行 这样矩阵 X 就是一个 m*(n+1) 维矩阵

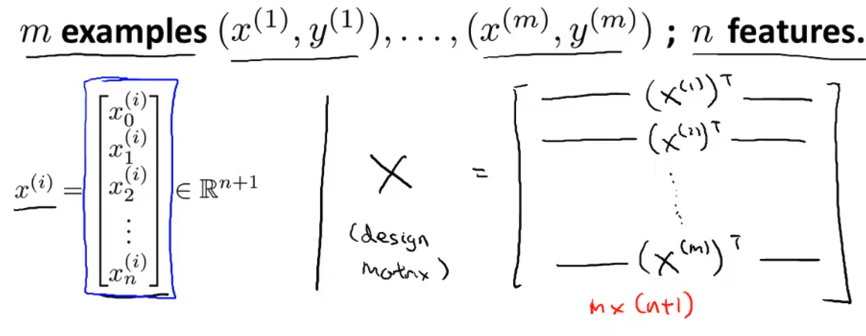
• 举个具体的例子 假如我只有一个特征变量 就是说除了 x0 之外只有一个特征变量 而 x0 始终为1 所以如果我的特征向量 xi等于1 也就是x0 和某个实际的特征变量 比如说房屋大小 那么我的设计矩阵 X 会是这样 第一行 就是这个的转置 所以最后得到1 然后 x(1)1 对于第二行 我们得到1 然后 x(1)2 这样直到1 然后 x(1)m 这就会是一个 m*2 维矩阵

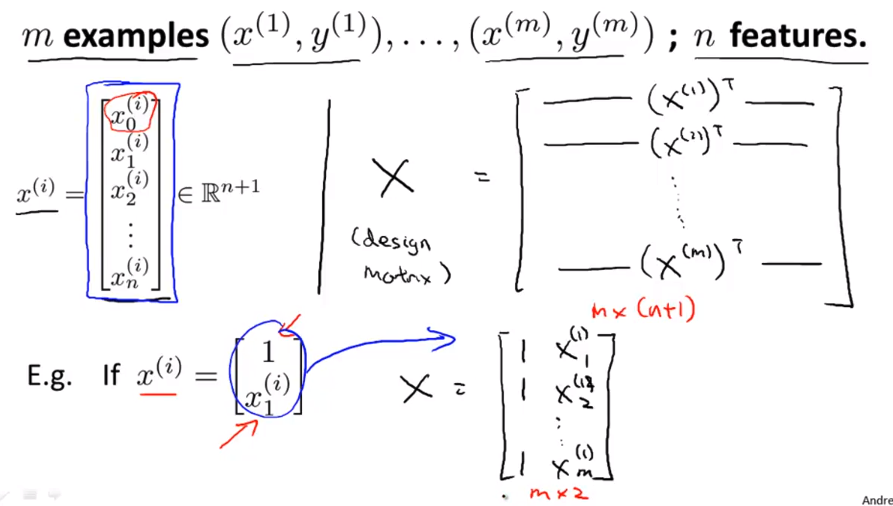
• 所以 这就是如何构建矩阵X 和向量y 有时我可能会在上面画一个箭头 来表示这是一个向量 但很多时候 我就只写y 是一样的 向量y 是这样求得的 把所有标签 所有训练集中正确的房子价格 放在一起 得到一个 m 维向量 y

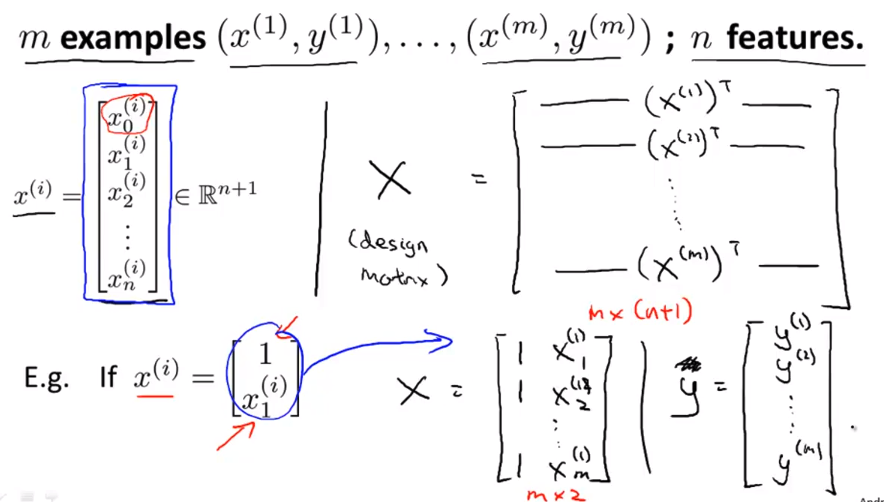
• 最后 构建完矩阵 X 和向量 y 我们就可以通过计算 X转置 乘以X的逆 乘以X转置 乘以y 来得到θ

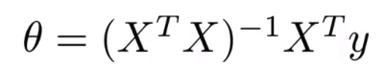
• 我现在就想确保你明白这个等式 并且知道如何实现它 所以具体来说 什么是 X 的转置乘以 X 的逆？ X的转置 乘以 X的逆 是 X转置 乘以X的逆矩阵 具体来说 如果你令A等于 X转置乘以X X的转置是一个矩阵 阵 我们把这个矩阵称为 A 那么 X转置乘以X的逆 就是矩阵 A 的逆 也就是 1/A 这就是计算过程 先计算 X转置乘以X 然后计算它的逆

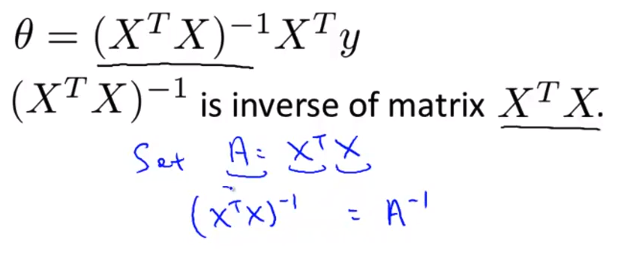
• 我们还没有谈到Octave 我们将在之后的视频中谈到这个 但是在 Octave 编程语言 或者类似的 MATLAB 编程语言里 计算这个量的命令是基本相同的 X转置 乘以X的逆 乘以X转置 乘以y 的代码命令如下所示

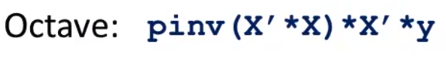
• 在 Octave 中 X’ 表示 X 转置 这个用红色框起来的表达式 计算的是 X 转置乘以 X 函数 pinv 是用来计算逆矩阵的函数 所以这个计算 X转置 乘以X的逆 然后乘以X转置 再乘以y 这样就算完了这个式子

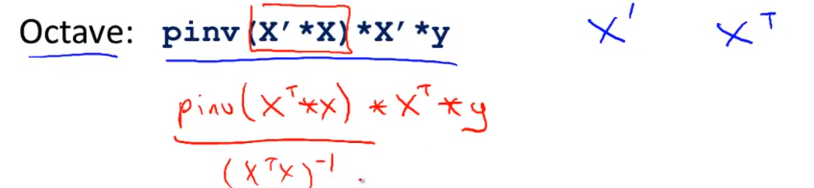
• 我没有证明这个式子 尽管我并不打算这么做 但是数学上是可以证明的 这个式子会给出最优的 θ 值 就是说如果你令 θ 等于这个 就是说如果你令 θ 等于这个 这个 θ 值会最小化这个线性回归的代价函数 J(θ)
• 最后一点 在之前视频中我提到特征变量归一化 和让特征变量在相似的范围内的想法 将所有的值归一化在类似范围内 如果你使用正规方程法 那么就不需要归一化特征变量 实际上这是没问题的 如果某个特征变量 x1 在 0到1的区间 某个特征变量 x2 在0到1000的区间 某个特征变量x3 在0到10^-5的区间 然后如果使用正规方程法 这样就没有问题 不需要做特征变量归一化 但如果你使用梯度下降法 特征变量归一化就很重要

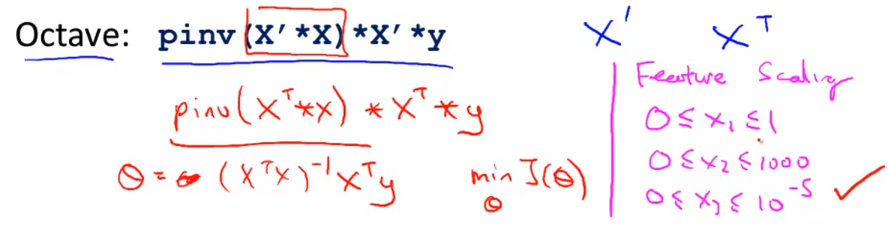
• 最后 你何时应该使用梯度下降法 而何时应该使用正规方程法呢？ 这里列举了一些它们的优点和缺点 假如你有 m 个训练样本和 n 个特征变量 梯度下降法的缺点之一就是 你需要选择学习速率 α 这通常表示需要运行多次 尝试不同的学习速率 α 然后找到运行效果最好的那个 所以这是一种额外的工作和麻烦 梯度下降法的另一个缺点是 它需要更多次的迭代 因为一些细节 计算可能会更慢 我们一会儿会看到更多的东西

• 至于正规方程 你不需要选择学习速率 α 所以就非常方便 也容易实现 你只要运行一下 通常这就够了 并且你也不需要迭代 所以不需要画出 $J(\theta)$ 的曲线 来检查收敛性或者采取所有的额外步骤 到目前为止 天平似乎倾向于正规方程法

• 这里列举一些正规方程法的缺点 和梯度下降法的优点 梯度下降法在有很多特征变量的情况下也能运行地相当好 所以即使你有上百万的特征变量 所以即使你有上百万的特征变量 你可以运行梯度下降法 并且通常很有效 它会正常的运行 相对地 正规方程法 为了求解参数θ 需要求解这一项 我们需要计算这项 X转置乘以X的逆 这个是一个 n*n 的矩阵 如果你有 n 个特征变量的话 因为如果你看一下 X转置乘以X 的维度 你可以发现他们的积的维度 X转置乘以X 是一个 n*n 的矩阵 其中 n是特征变量的数量 实现逆矩阵计算所需要的计算量 大致是矩阵维度的三次方 因此计算这个逆矩阵需要计算大致 n 的三次方 有时稍微比计算 n 的三次方快一些 但是对我们来说很接近 所以如果特征变量的数量 n 很大的话 那么计算这个量会很慢 实际上标准方程法会慢很多 因此如果 n 很大 我可能还是会使用梯度下降法 因为我们不想花费 n 的三次方的时间 但如果 n 比较小 那么标准方程法可能更好地求解参数 θ

• 那么怎么叫大或者小呢？ 那么 如果 n 是上百的 计算百位数乘百位数的矩阵 对于现代计算机来说没有问题 如果 n 是上千的 我还是会使用正规方程法 千位数乘千位数的矩阵做逆变换 对于现代计算机来说实际上是非常快的 但如果 n 上万 那么我可能会开始犹豫 上万乘上万维的矩阵作逆变换 会开始有点慢 此时我可能开始倾向于 梯度下降法 但也不绝对 n 等于一万 你可以 逆变换一个一万乘一万的矩阵 但如果 n 远大于此 我可能就会使用梯度下降法了 所以如果 n 等于10^6 有一百万个特征变量 那么做百万乘百万的矩阵的逆变换 就会变得非常费时间 在这种情况下我一定会使用梯度下降法 所以很难给出一个确定的值 来决定何时该换成梯度下降法 但是 对我来说通常是 在一万左右 我会开始考虑换成梯度下降法 或者我们将在以后讨论到的其他算法

• 总结一下 只要特征变量的数目并不大 正规方程是一个很好的 计算参数 θ 的替代方法 具体地说 只要特征变量数量小于一万 我通常使用正规方程法 而不使用梯度下降法 预告一下在之后的课程中我们要讲的 随着我们要讲的学习算法越来越复杂 例如 当我们讲到分类算法 像逻辑回归算法 我们会看到 实际上对于那些算法 并不能使用正规方程法 对于那些更复杂的学习算法 我们将不得不仍然使用梯度下降法 因此 梯度下降法是一个非常有用的算法 可以用在有大量特征变量的线性回归问题 或者我们以后在课程中 会讲到的一些其他的算法 因为 标准方程法不适合或者不能用在它们上 但对于这个特定的线性回归模型 正规方程法是一个 比梯度下降法更快的替代算法 所以 根据具体的问题 所以 以及你的特征变量的数量 这两算法都是值得学习的

  正规方程笔记

到目前为止，我们都在使用梯度下降算法，但是对于某些线性回归问题，正规方程方法是更好的解决方案。如：

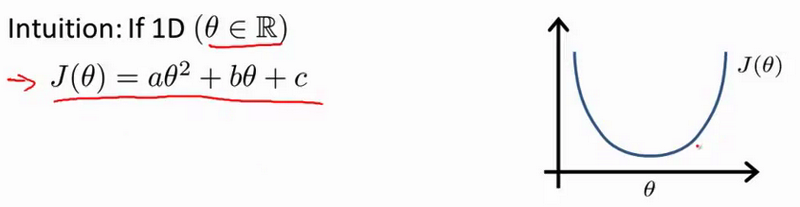
正规方程是通过求解下面的方程来找出使得代价函数最小的参数的：$\frac{\partial}{\partial{\theta_{j}}}J\left( {\theta_{j}} \right)=0$ 。
假设我们的训练集特征矩阵为 $X$（包含了 ${{x}_{0}}=1$）并且我们的训练集结果为向量 $y$，则利用正规方程解出向量 $\theta ={{\left( {X^T}X \right)}^{-1}}{X^{T}}y$ 。
上标T代表矩阵转置，上标-1 代表矩阵的逆。设矩阵$A={X^{T}}X$，则：${{\left( {X^T}X \right)}^{-1}}={A^{-1}}$
以下表示数据为例：

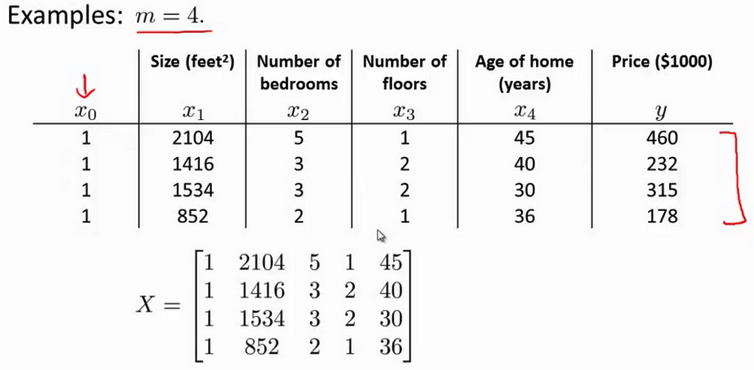
即：

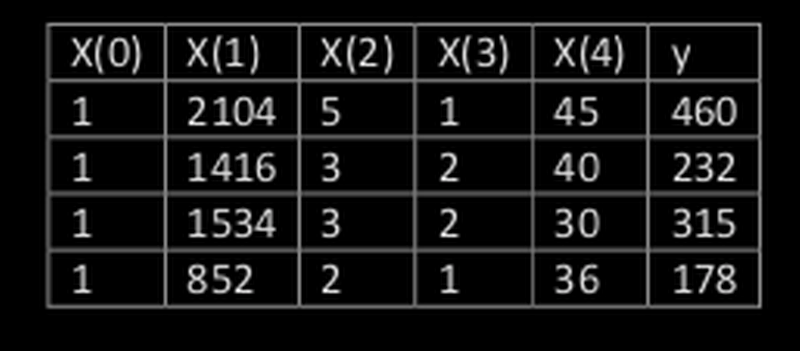
运用正规方程方法求解参数：

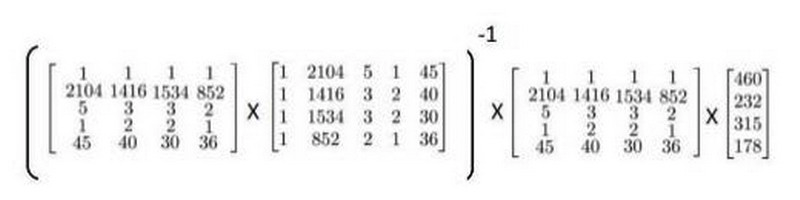
在 Octave 中，正规方程写作：

pinv(X'*X)*X'*y

注：对于那些不可逆的矩阵（通常是因为特征之间不独立，如同时包含英尺为单位的尺寸和米为单位的尺寸两个特征，也有可能是特征数量大于训练集的数量），正规方程方法是不能用的。

梯度下降与正规方程的比较：

梯度下降	正规方程
需要选择学习率{% raw %}$\alpha${% endraw %}	不需要
需要多次迭代	一次运算得出
当特征数量{% raw %}$n${% endraw %}大时也能较好适用	需要计算{% raw %}${{\left( {{X}^{T}}X \right)}^{-1}}${% endraw %} 如果特征数量n较大则运算代价大，因为矩阵逆的计算时间复杂度为{% raw %}$O\left( {{n}^{3}} \right)${% endraw %}，通常来说当{% raw %}$n${% endraw %}小于10000 时还是可以接受的
适用于各种类型的模型	只适用于线性模型，不适合逻辑回归模型等其他模型

总结一下，只要特征变量的数目并不大，标准方程是一个很好的计算参数{% raw %}$\theta ${% endraw %}的替代方法。具体地说，只要特征变量数量小于一万，我通常使用标准方程法，而不使用梯度下降法。

随着我们要讲的学习算法越来越复杂，例如，当我们讲到分类算法，像逻辑回归算法，我们会看到，
实际上对于那些算法，并不能使用标准方程法。对于那些更复杂的学习算法，我们将不得不仍然使用梯度下降法。因此，梯度下降法是一个非常有用的算法，可以用在有大量特征变量的线性回归问题。或者我们以后在课程中，会讲到的一些其他的算法，因为标准方程法不适合或者不能用在它们上。但对于这个特定的线性回归模型，标准方程法是一个比梯度下降法更快的替代算法。所以，根据具体的问题，以及你的特征变量的数量，这两种算法都是值得学习的。

正规方程的python实现：

import numpy as np

def normalEqn(X, y):

   theta = np.linalg.inv(X.T@X)@X.T@y #X.T@X等价于X.T.dot(X)

   return theta

正规方程及不可逆性

在这段视频中谈谈正规方程 ( normal equation )，以及它们的不可逆性。
由于这是一种较为深入的概念，并且总有人问我有关这方面的问题，因此，我想在这里来讨论它，由于概念较为深入，所以对这段可选材料大家放轻松吧，也许你可能会深入地探索下去，并且会觉得理解以后会非常有用。但即使你没有理解正规方程和线性回归的关系，也没有关系。

我们要讲的问题如下：$\theta ={{\left( {X^{T}}X \right)}^{-1}}{X^{T}}y$

有些同学曾经问过我，当计算 $\theta$=inv(X'X ) X'y ，那对于矩阵$X'X$的结果是不可逆的情况咋办呢?
如果你懂一点线性代数的知识，你或许会知道，有些矩阵可逆，而有些矩阵不可逆。我们称那些不可逆矩阵为奇异或退化矩阵。

问题的重点在于$X'X$的不可逆的问题很少发生，在Octave里，如果你用它来实现$\theta$的计算，你将会得到一个正常的解。在Octave里，有两个函数可以求解矩阵的逆，一个被称为pinv()，另一个是inv()，这两者之间的差异是些许计算过程上的，一个是所谓的伪逆，另一个被称为逆。使用pinv() 函数可以展现数学上的过程，这将计算出$\theta$的值，即便矩阵$X'X$是不可逆的。

在pinv() 和 inv() 之间，又有哪些具体区别呢 ?

其中inv() 引入了先进的数值计算的概念。

出现不可逆的一般有两个原因,第一个原因是:如果不知何故,再你的学习问题中,你有多余的功能 例如，在预测住房价格时，如果${x_{1}}$是以英尺为尺寸规格计算的房子，${x_{2}}$是以平方米为尺寸规格计算的房子，同时，你也知道1米等于3.28英尺 ( 四舍五入到两位小数 )，这样，你的这两个特征值将始终满足约束：${x_{1}}={x_{2}}*{{\left( 3.28 \right)}^{2}}$。 实际上，你可以用这样的一个线性方程，来展示那两个相关联的特征值，矩阵X'X将是不可逆的。

第二个原因是，在你想用大量的特征值，尝试实践你的学习算法的时候，可能会导致矩阵$X'X$的结果是不可逆的。 具体地说，在$m$小于或等于n的时候，例如，有$m$等于10个的训练样本也有$n$等于100的特征数量。要找到适合的$(n +1)$ 维参数矢量$\theta$，这将会变成一个101维的矢量，尝试从10个训练样本中找到满足101个参数的值，这工作可能会让你花上一阵子时间，但这并不总是一个好主意。因为，正如我们所看到你只有10个样本，以适应这100或101个参数，数据还是有些少。

稍后我们将看到，如何使用小数据样本以得到这100或101个参数，通常，我们会使用一种叫做正则化的线性代数方法，通过删除某些特征或者是使用某些技术，来解决当$m$比$n$小的时候的问题。即使你有一个相对较小的训练集，也可使用很多的特征来找到很多合适的参数。

总之当你发现的矩阵$X'X$的结果是奇异矩阵，或者找到的其它矩阵是不可逆的，我会建议你这么做。

首先，看特征值里是否有一些多余的特征，像这些${x_{1}}$和${x_{2}}$是线性相关的，互为线性函数。同时，当有一些多余的特征时，可以删除这两个重复特征里的其中一个，无须两个特征同时保留，将解决不可逆性的问题。因此，首先应该通过观察所有特征检查是否有多余的特征，如果有多余的就删除掉，直到他们不再是多余的为止，如果特征数量实在太多，我会删除些 用较少的特征来反映尽可能多内容，否则我会考虑使用正规化方法。
如果矩阵$X'X$是不可逆的，（通常来说，不会出现这种情况），如果在Octave里，可以用伪逆函数pinv() 来实现。这种使用不同的线性代数库的方法被称为伪逆。即使$X'X$的结果是不可逆的，但算法执行的流程是正确的。总之，出现不可逆矩阵的情况极少发生，所以在大多数实现线性回归中，出现不可逆的问题不应该过多的关注${X^{T}}X$是不可逆的。

增加内容：

$\theta ={{\left( {X^{T}}X \right)}^{-1}}{X^{T}}y$ 的推导过程： $J\left( \theta \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( {h_{\theta}}\left( {x^{(i)}} \right)-{y^{(i)}} \right)}^{2}}}$

其中：${h_{\theta}}\left( x \right)={\theta^{T}}X={\theta_{0}}{x_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}}$

将向量表达形式转为矩阵表达形式，则有$J(\theta )=\frac{1}{2}{{\left( X\theta -y\right)}^{2}}$ ，其中$X$为$m$行$n$列的矩阵（$m$为样本个数，$n$为特征个数），$\theta$为$n$行1列的矩阵，$y$为$m$行1列的矩阵，对$J(\theta )$进行如下变换

$J(\theta )=\frac{1}{2}{{\left( X\theta -y\right)}^{T}}\left( X\theta -y \right)$

​ $=\frac{1}{2}\left( {{\theta }^{T}}{{X}^{T}}-{{y}^{T}} \right)\left(X\theta -y \right)$

​ $=\frac{1}{2}\left( {{\theta }^{T}}{{X}^{T}}X\theta -{{\theta}^{T}}{{X}^{T}}y-{{y}^{T}}X\theta -{{y}^{T}}y \right)$

接下来对$J(\theta )$偏导，需要用到以下几个矩阵的求导法则:

$\frac{dAB}{dB}={{A}^{T}}$ $\frac{d{{X}^{T}}AX}{dX}=2AX$

所以有:

$\frac{\partial J\left( \theta \right)}{\partial \theta }=\frac{1}{2}\left(2{{X}^{T}}X\theta -{{X}^{T}}y -{{X}^{T}}y -0 \right)$

​ $={{X}^{T}}X\theta -{{X}^{T}}y$

令$\frac{\partial J\left( \theta \right)}{\partial \theta }=0$,

则有$\theta ={{\left( {X^{T}}X \right)}^{-1}}{X^{T}}y$