第二章 单变量线性回归(Linear Regression with One Variable)

Gradient Descennt

我们已经定义了代价函数J 而在这段视频中 我想向你们介绍梯度下降这种算法 这种算法可以将代价函数$J$最小化 梯度下降是很常用的算法 它不仅被用在线性回归上 它实际上被广泛的应用于机器学习领域中的众多领域 在后面课程中 为了解决其他线性回归问题 我们也也将使用梯度下降法 最小化其他函数 而不仅仅是只用在本节课的代价函数$J$ 因此在这个视频中 我将讲解用梯度下降算法最小化函数 $J$在后面的视频中 我们还会将此算法应用于具体的 代价函数J中来解决线性回归问题 下面是问题概述

• 在这里 我们有一个函数 $J(\theta_0, \theta_1)$ 也许这是一个线性回归的代价函数 也许是一些其他函数 要使其最小化 我们需要用一个算法 来最小化函数$J(\theta_0, \theta_1)$ 就像刚才说的 事实证明 梯度下降算法可应用于 多种多样的函数求解 所以想象一下如果你有一个函数$J(\theta_0, \theta_1,…,\theta_n)$ 你希望可以通过最小化 $\theta_0$到$\theta_n$来最小化此代价函数$J(\theta_0, \theta_1,…,\theta_n)$ 用n个$\theta$是为了证明梯度下降算法可以解决更一般的问题 但为了简洁起见 为了简化符号 在接下来的视频中 我只用两个参数
• 下面就是关于梯度下降的构想 我们要做的是 我们要开始对$\theta_0$和$\theta_1$ 进行一些初步猜测(也就是初始化) 它们到底是什么其实并不重要 但通常的选择是将 $\theta_0$设为0 将$\theta_1$也设为0 将它们都初始化为0 我们在梯度下降算法中要做的 就是不停地一点点地改变 $\theta_0$和$\theta_1$ 试图通过这种改变使得$J(\theta_0, \theta_1)$变小 直到我们找到 $J$ 的最小值 或许是局部最小值

• 让我们通过一些图片来看看梯度下降法是如何工作的 我在试图让这个函数值最小 注意坐标轴 $\theta_0$和$\theta_1$在水平轴上 而函数 $J$在垂直坐标轴上 图形表面高度则是 $J$的值

• 我们希望最小化这个函数 所以我们从 $\theta_0$ 和 $\theta_1$ 的某个值出发 所以想象一下 对 $\theta_0$和$\theta_1$赋以某个初值 也就是对应于从这个函数表面上的某个起始点出发 对吧 所以不管 $\theta_0$和$\theta_1$的取值是多少 我将它们初始化为0 但有时你也可把它初始化为其他值 现在我希望大家把这个图像想象为一座山 想像类似这样的景色 公园中有两座山 想象一下你正站立在山的这一点上 站立在你想象的公园这座红色山上 在梯度下降算法中 我们要做的就是旋转360度 看看我们的周围 并问自己 我要在某个方向上 用小碎步尽快下山 这些小碎步需要朝什么方向?
• 如果我们站在山坡上的这一点 你看一下周围 你会发现最佳的下山方向 大约是那个方向 好的 现在你在山上的新起点上

• 你再看看周围 然后再一次想想 我应该从什么方向迈着小碎步下山? 然后你按照自己的判断又迈出一步 往那个方向走了一步

• 然后重复上面的步骤 从这个新的点 你环顾四周 并决定从什么方向将会最快下山 然后又迈进了一小步 又是一小步 并依此类推 直到你接近这里 直到局部最低点的位置

• 此外 这种下降有一个有趣的特点 第一次我们是从这个点开始进行梯度下降算法的 是吧 在这一点上从这里开始 现在想象一下 我们在刚才的右边一些的位置 对梯度下降进行初始化 想象我们在右边高一些的这个点 开始使用梯度下降 如果你重复上述步骤 停留在该点 并环顾四周 往下降最快的方向迈出一小步 然后环顾四周 又迈出一步 然后如此往复 如果你从右边不远处开始 梯度下降算法将会带你来到 这个右边的第二个局部最优处

• 如果从刚才的第一个点出发 你会得到这个局部最优解 但如果你的起始点偏移了一些 起始点的位置略有不同 你会得到一个 非常不同的局部最优解 这就是梯度下降算法的一个特点 我们会在之后继续探讨这个问题

• 好的 这是我们从图中得到的直观感受 看看这个图 这是梯度下降算法的定义 我们将会反复做这些 直到收敛

• 我们要更新参数 $\theta_j$ 方法是 用 $\theta_j$ 减去 $\alpha$乘以这一部分
  • := 表示赋值 这是一个赋值运算符
  • 等号 = :写出a=b 那么这是一个判断为真的声明 如果我写 a=b 就是在断言 a的值是等于 b的值的 这是声明 声明 a的值 与b的值相同
  • α :一个数字 被称为学习速率
    • 什么是$\alpha$呢? 在梯度下降算法中 它控制了 我们下山时会迈出多大的步子 因此如果 $\alpha$值很大 那么相应的梯度下降过程中 我们会试图用大步子下山 如果$\alpha$值很小 那么我们会迈着很小的小碎步下山 关于如何设置 $\alpha$的值等内容 在之后的课程中 我会回到这里并且详细说明 $\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1)$
  • 最后 是公式的这一部分$\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1)$ 这是一个微分项 我现在不想谈论它 但我会推导出这个微分项 并告诉你到底这要如何计算 你们中有人大概比较熟悉微积分 但即使你不熟悉微积分 也不用担心 我会告诉你 对这一项 你最后需要做什么
• 现在 在梯度下降算法中 还有一个更微妙的问题 在梯度下降中 我们要更新 $\theta_0$ 和 $\theta_1$ 当 j=0 和 j=1 时 会产生更新 所以你将更新 $\theta_0$ 和 $\theta_1$ 实现梯度下降算法的微妙之处是 在这个表达式中 如果你要更新这个等式 你需要同时更新 $\theta_0$ 和 $\theta_1$ 实现方法是 你应该计算公式右边的部分 通过那一部分计算出$\theta_0$ 和 $\theta_1$的值 然后同时更新 $\theta_0$ 和 $\theta_1$ 让我进一步阐述这个过程
• 在梯度下降算法中 下图是正确实现同时更新的方法 我要设 temp0等于这些 设temp1等于那些 所以首先计算出公式右边这一部分 然后将计算出的结果 一起存入 temp0和 temp1 之中 然后同时更新 θ0和θ1 因为这才是正确的实现方法

• 与此相反 下面是不正确的实现方法 因为它没有做到同步更新 在这种不正确的实现方法中 我们计算 temp0 然后我们更新 $\theta_0$ 然后我们计算 temp1 然后我们将 temp1 赋给θ1 右边的方法和左边的区别是 让我们看这里 就是这一步 如果这个时候你已经更新了θ0 那么你会使用 θ0的新的值来计算这个微分项 所以由于你已经在这个公式中使用了新的 θ0的值 那么这会产生一个与左边不同的 temp1的值 所以右边并不是正确地实现梯度下降的做法

• 我不打算解释为什么你需要同时更新 同时更新是梯度下降中的一种常用方法 我们之后会讲到 实际上同步更新是更自然的实现方法 当人们谈到梯度下降时 他们的意思就是同步更新 如果用非同步更新去实现算法 代码可能也会正确工作 但是右边的方法并不是人们所指的那个梯度下降算法 而是具有不同性质的其他算法 由于各种原因 这其中会表现出微小的差别 你应该做的是 在梯度下降中真正实现同时更新 这些就是梯度下降算法的梗概

• 在接下来的视频中 我们要进入这个微分项的细节之中 我已经写了出来但没有真正定义 如果你已经修过微积分课程 如果你熟悉偏导数和导数 这其实就是这个微分项 如果你不熟悉微积分 不用担心 即使你之前没有看过微积分 或者没有接触过偏导数 在接下来的视频中 你会得到一切你需要知道的 如何计算这个微分项的知识 下一个视频中 希望我们能够给出 实现梯度下降算法的所有知识

小小的总结–Gradient Descennt(梯度下降)

• 在假设函数中，我们需要估计假设函数中的参数。这就是梯度下降的地方。

• x轴表示$\theta_0$，y轴表示$\theta_1$，z轴上表示$J(\theta_0,\theta_1)$代价函数。我们图上的点是 给定$\theta_0$和$\theta_1$ 代价函数的值。

• 当我们的代价函数处于图的底部时，即当其值是局部最小时，表示我们已经找到正确的$\theta_0$和$\theta_1$。红色箭头显示图表中的最小点。

• 我们这样做的方式是通过获取代价函数的导数（函数的切线）。切线的斜率是该点的导数，它会给我们一个走向的方向。我们逐步降低成本函数的下降速度。每一步的大小由参数α决定，称为学习率。

• 例如，上图中每个“星号”之间的距离代表由我们的参数α确定的一个步骤。 α越小，步长越小，α越大，步长越大。步进的方向取决于$J(\theta_0,\theta_1)$ 的偏导数。根据图表的起始位置，可能会出现不同的点。上面的图片向我们展示了两个不同的起点，最终在两个不同的地方。

• 梯度下降算法是：
  重复，直到收敛：
  j = 0,1代表特征索引号。

• 在每次迭代j中，应同时更新参数$\theta_1,\theta_2,…\theta_n$。在计算第j次迭代之前更新特定参数会导致错误的实现。

Gradient Descent Intuition

在之前的视频中 我们给出了一个数学上关于梯度 下降的定义 本次视频我们更深入研究一下 更直观地感受一下这个 算法是做什么的 以及梯度下降算法的更新过程有什么意义 这是我们上次视频中看到的梯度下降算法 提醒一下 这个参数 α 术语称为学习速率 它控制我们以多大的幅度更新这个参数θj. 第二部分是导数项 而我在这个视频中要做的就是 给你一个更直观的认识 这两部分有什么用 以及 为什么当把 这两部分放一起时 整个更新过程是有意义的

• 为了更好地让你明白 我要做是用一个稍微简单的例子 比如我们想最小化的那个 函数只有一个参数的情形 所以 假如我们有一个代价函数J 只有一个参数 θ1 就像我们前几次视频中讲的 $\theta_1$是一个实数 对吧？那么我们可以画出一维的曲线 看起来很简单 让我们试着去理解 为什么梯度下降法 会在这个函数上起作用

• 所以 假如这是我的函数 关于$\theta_1$的函数$J(\theta_1)$是一个实数 对吧？ 现在我们已经对这个蓝色点上用于梯度下降法的$\theta_1$ 进行了初始化 想象一下在我的函数图像上 从那个点出发 那么梯度下降 要做的事情是不断更新 $\theta_1$ 等于$\theta_1$ 减$\alpha$ 倍的 $\frac{d}{d\theta_1}J(\theta_1)$ 这个项 对吧？哦 顺便插一句 你知道 这个微分项是吧？可能你想问为什么我改变了符号 之前用的是偏导数的符号 如果你不知道偏导数的符号 和$\frac{d}{d\theta}$之间的区别是什么 不用担心 从技术上讲 在数学中 我们称这是一个偏导数 这是一个导数 这取决于函数J的参数数量 但是这是一个 数学上的区别 就本课的目标而言 可以默认为 这些偏导数符号 和$\frac{d}{d\theta}$是完全一样的东西 不用担心 是否存在任何差异 我会尽量使用数学上的 精确的符号 但就我们的目的而言 这些符号是没有区别的

• 好的 那么我们来看这个方程 我们要计算 这个导数 求导的目的 基本上可以说 取红色一点的切线 就是这样一条红色的直线 刚好与函数相切于这一点 让我们看看这条红色直线的斜率 其实这就是导数 也就是说 直线的斜率 也就是这条 刚好与函数曲线相切的这条直线 这条直线的斜率正好是 这个高度除以这个水平长度 现在 这条线有 一个正斜率 也就是说它有正导数 因此 我得到的新的$\theta_1$ $\theta_1$更新后等于$\theta_1$减去一个正数乘以$\alpha$. $\alpha$ 也就是学习速率也是一个正数 所以 我要使$\theta_1$减去一个东西 所以相当于我将$\theta_1$向左移 使$\theta_1$变小了

• 我们可以看到 这么做是对的 因为实际上我往这个方向移动 确实让我更接近那边的最低点 所以 梯度下降到目前为止似乎 是在做正确的事
• 让我们来看看另一个例子 让我们用同样的函数$J$ 同样再画出函数$J(\theta_1)$的图像 而这次 我们把参数初始化到左边红色这点 所以$\theta_1$ 在这里 同样把这点对应到曲线上 现在 导数项$\frac{d}{d\theta_1}J(\theta_1)$ 在这点上计算时 看上去会是红色这条线的斜率 这个导数是这条线的斜率 但是这条线向下倾斜 所以这条线具有负斜率 对吧？ 或者说 这个函数有负导数 也就意味着在那一点上有负斜率 因此 这个导数项小于等于零 所以 当我更新$\theta$时, $\theta$被更新为$\theta$减去$\alpha$乘以一个负数 因此我是在用 $\theta_1$减去一个负数 这意味着我实际上是在增加$\theta_1$ 对不对？因为这是减去一个负数 意味着给$\theta$加上一个数 这就意味着最后我实际上增加了$\theta$的值 因此 我们将 从这里开始 增加$\theta$ 似乎这也是我希望得到的 也就是 让我更接近最小值了

• 所以 我希望这样很直观地给你解释了 导数项的意义 让我们接下来再看一看学习速率$\alpha$ 我们来研究一下它有什么用 这就是我梯度下降法的 更新规则 就是这个等式 让我们来看看如果$\alpha$ 太小或 $\alpha$ 太大 会出现什么情况 这第一个例子 $\alpha$太小会发生什么呢 这是我的函数$J(\theta)$ 就从这里开始 如果$\alpha$太小了 那么我要做的是要去 用一个比较小的数乘以更新的值 所以最终 它就像一个小宝宝的步伐 这是一步 然后从这个新的起点开始 迈出另一步 但是由于$\alpha$ 太小 因此只能迈出另一个 小碎步 所以如果我的学习速率太小 结果就是 只能这样像小宝宝一样一点点地挪动 去努力接近最低点 这样就需要很多步才能到达最低点 所以如果$\alpha$ 太小的话 可能会很慢 因为它会一点点挪动 它会需要 很多步才能到达全局最低点

• 那么如果$\alpha$ 太大又会怎样呢 这是我的函数$J(\theta)$ 如果$\alpha$ 太大 那么梯度下降法可能会越过最低点 甚至可能无法收敛 我的意思是 比如我们从这个点开始 实际上这个点已经接近最低点 因此导数指向右侧 但如果$\alpha$ 太大的话 我会迈出很大一步 也许像这样巨大的一步 对吧？所以我最终迈出了一大步 现在 我的代价函数变得更糟 因为离这个最低点越来越远 现在我的导数指向左侧 实际上在减小$\theta$ 但是你看 如果我的学习速率过大 我会移动一大步 从这点一下子又到那点了 对吗？如果我的学习率太大 下一次迭代 又移动了一大步 越过一次 又越过一次 一次次越过最低点 直到你发现 实际上 离最低点越来越远 所以 如果$\alpha$太大 它会导致无法收敛 甚至发散

• 现在 我还有一个问题 这问题挺狡猾的 如果我们预先把$\theta_1$ 放在一个局部的最低点 你认为下一步梯度下降法会怎样工作？ 所以假设你将$\theta_1$初始化在局部最低点 假设这是你的$\theta_1$的初始值 在这儿 它已经在一个局部的 最优处或局部最低点 结果是局部最优点的导数 将等于零 因为它是那条切线的斜率 而这条线的斜率将等于零 因此 此导数项等于0 因此 在你的梯度下降更新过程中 你有一个$\theta_1$ 然后用$\theta_1$ 减$\alpha$ 乘以0来更新$\theta_1$ 所以这意味着什么 这意味着你已经在局部最优点 它使得$\theta_1$不再改变 也就是新的$\theta_1$等于原来的$\theta_1$ 因此 如果你的参数已经处于 局部最低点 那么梯度下降法更新其实什么都没做 它不会改变参数的值 这也正是你想要的 因为它使你的解始终保持在 局部最优点 这也解释了为什么即使学习速率$\alpha$ 保持不变时 梯度下降也可以收敛到局部最低点 我想说的是这个意思

• 我们来看一个例子 这是代价函数$J(\theta)$ 我想找到它的最小值 首先初始化我的梯度下降算法 在那个品红色的点初始化 如果我更新一步梯度下降 也许它会带我到绿色这个点 因为这个点的导数是相当陡的 现在 在这个绿色的点 如果我再更新一步 你会发现我的导数 也即斜率 相比于在品红点 是没那么陡的 对吧？因为随着我接近最低点 我的导数越来越接近零 所以 梯度下降一步后 新的导数会变小一点点 然后我想再梯度下降一步 在这个绿点我自然会用一个稍微 跟刚才在那个品红点时比 再小一点的一步 现在到了新的点 红色点 更接近全局最低点了 因此这点的导数会比在绿点时更小 所以 我再进行一步梯度下降时 我的导数项是更小的 $\theta_1$更新的幅度就会更小 所以你会移动更小的一步 像这样 随着梯度下降法的运行 你移动的幅度会自动变得越来越小 直到最终移动幅度非常小 你会发现 已经收敛到局部极小值 所以回顾一下 在梯度下降法中 当我们接近局部最低点时 梯度下降法会自动采取 更小的幅度 这是因为当我们接近局部最低点时 很显然在局部最低时导数等于零 所以当我们 接近局部最低时 导数值会自动变得越来越小 所以梯度下降将自动采取较小的幅度 这就是梯度下降的做法 所以实际上没有必要再另外减小$\alpha$ 这就是梯度下降算法

• 你可以用它来最小化 最小化任何代价函数$J$ 不只是线性回归中的代价函数$J$ 在接下来的视频中 我们要用代价函数$J$ 回到它的本质 线性回归中的代价函数 也就是我们前面得出的平方误差函数 结合梯度下降法 以及平方代价函数 我们会得出第一个机器学习算法 即线性回归算法

小小的总结–Gradient Descent Intuition

• 在本视频中，我们探索了使用一个参数$\theta_1$并绘制其代价函数来实现梯度下降的场景。 我们的单一参数公式为：

• 无论 $\frac{d}{d\theta_1}J(\theta_1)$ 的斜率符号如何，$\theta_1$最终收敛到其最小值。 下图显示当斜率为负值时，$\theta_1$的值增加，当为正值时，$\theta_1$的值减小。

• 在附注中，我们应该调整参数α以确保梯度下降算法在合理的时间内收敛。 未能收敛或获得最小值的时间太多意味着我们的步长是错误的。

• 梯度下降如何以固定步长$\alpha$收敛？
  收敛背后的直觉是，当我们逼近我们的凸函数的底部时，$\frac{d}{d\theta_1}J(\theta_1)$接近0。 因此我们得到：

$\theta_1:=\theta_1-\alpha*0$

Gradient Descent For Linear Regression

在以前的视频中我们谈到 关于梯度下降算法 梯度下降是很常用的算法 它不仅被用在线性回归上 和线性回归模型、平方误差代价函数 在这段视频中 我们要 将梯度下降 和代价函数结合 在后面的视频中 我们将用到此算法 并将其应用于 具体的拟合直线的线性回归算法里 这就是 我们在之前的课程里所做的工作

• 这是梯度下降算法 这个算法你应该很熟悉 这是线性回归模型 还有线性假设和平方误差代价函数 我们将要做的就是 用梯度下降的方法 来最小化平方误差代价函数 为了 使梯度下降 为了 写这段代码 我们需要的关键项 是这里这个微分项

• 所以.我们需要弄清楚 这个偏导数项是什么 并结合这里的 代价函数$J$ 的定义 就是这样 一个求和项 代价函数就是 这个误差平方项 我这样做 只是 把定义好的代价函数 插入了这个微分式 再简化一下 这等于是 这一个求和项 $\theta_0+\theta_1x^{(i)}-y{(i)}$

• 实际上我们需要 弄清楚这两个 偏导数项是什么 这两项分别是 j=0 和j=1的情况 因此我们要弄清楚 $\theta_0$和 $\theta_1$ 对应的 偏导数项是什么 (将上面的式子平方化开再分别对$\theta_0$和 $\theta_1$求偏导)

最终结果如下:

• 所以 偏导数项 从这个等式 到下面的等式 计算这些偏导数项需要一些多元微积分 如果你掌握了微积分 你可以随便自己推导这些 然后你检查你的微分 你实际上会得到我给出的答案 但如果你 不太熟悉微积分 别担心 你可以直接用这些 已经算出来的结果 你不需要掌握微积分 或者别的东西 来完成作业 你只需要会用梯度下降就可以

• 在定义这些以后 在我们算出 这些微分项以后 这些微分项 实际上就是代价函数J的斜率 现在可以将它们放回 我们的梯度下降算法 所以这就是专用于 线性回归的梯度下降 反复执行括号中的式子直到收敛 $\theta_0$和$\theta_1$不断被更新 都是加上一个$-\frac{\alpha}{m}$ 乘上后面的求和项 所以这里这一项 所以这就是我们的线性回归算法

• 这一项就是关于$\theta_0$的偏导数 在上一张幻灯片中推出的

• 而第二项 这一项是刚刚的推导出的 关于$\theta_1$的 偏导数项

• 提醒一下 执行梯度下降时 有一个细节要注意 就是必须要 同时更新$\theta_0$和$\theta_1$
• 所以 让我们来看看梯度下降是如何工作的 我们用梯度下降解决问题的 一个原因是 它更容易得到局部最优值 当我第一次解释梯度下降时 我展示过这幅图

• 在表面上 不断下降 并且我们知道了 根据你的初始化 你会得到不同的局部最优解 你知道.你可以结束了.在这里或这里。

• 但是 事实证明 用于线性回归的 代价函数 总是这样一个 弓形的样子

• 这个函数的专业术语是 这是一个凸函数 我不打算在这门课中 给出凸函数的定义 凸函数(convex function) 但不正式的说法是 它就是一个弓形的函数 因此 这个函数 没有任何局部最优解 只有一个全局最优解 并且无论什么时候 你对这种代价函数 使用线性回归 梯度下降法得到的结果 总是收敛到全局最优值 因为没有全局最优以外的其他局部最优点
• 现在 让我们来看看这个算法的执行过程 像往常一样 这是假设函数的图 还有代价函数J的图

• 让我们来看看如何 初始化参数的值 通常来说 初始化参数为零 $\theta_0$和$\theta_1$都在零 但为了展示需要 在这个梯度下降的实现中 我把$\theta_0$初始化为-900 $\theta_1$初始化为-0.1
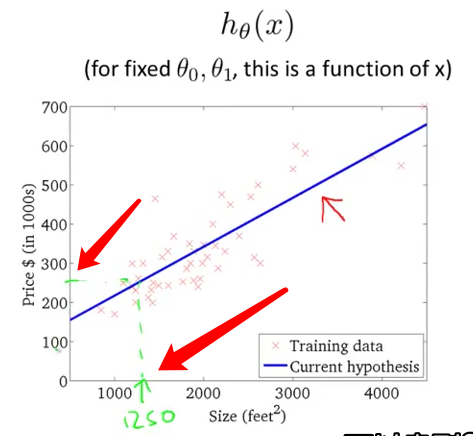
• 这对应的假设$h(x)$ 就应该是下图左边 $h(x)=-900-0.1x$ 代价函数$J(\theta_0,\theta_1)$对应的是下图右边

• 现在 如果我们进行一次梯度下降,从一点开始向左下方移动一小步,然后就得到了第二个点,可以看到,这第二点假设函数的线相对于第一点假设函数的线改变了一点点.

• 然后就是不断的移动代价函数的点,梯度不断下降,假设函数越来越拟合数据,直到收敛到全局最小值.这个全局最小值对应的假设函数 给出了最拟合数据的解 这就是梯度下降法

• 我们刚刚运行了一遍 并且最终得到了 房价数据的最好拟合结果 现在你可以用它来预测房价了 比如说 假如你有个朋友 他有一套房子 面积1250平方英尺(约116平米) 现在你可以通过这个数据 然后告诉他们 也许他的房子 可以卖到35万美元

• 最后 我想再给出 另一个名字 实际上 我们刚刚使用的算法 有时也称为批量梯度下降(Batch Gradient Descent),指的是,在梯度下降的每一步中,我们都用到了所有的训练样本
• 在梯度下降中,在计算微分求导项时,我们需要进行求和计算,所以在每一个单独的梯度计算中,我们最终都要计算这样一个东西—这个项需要对所有m个训练样本求和.

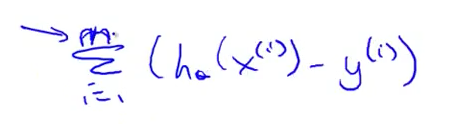
• 有些同学之前 可能已经学过 高等线性代数 你应该知道 有一种计算代价函数J最小值的数值解法 不需要梯度下降这种迭代算法 在后面的课程中 我们也会谈到这个方法 它可以在不需要多步梯度下降的情况下 也能解出代价函数J的最小值 这是另一种称为正规方程(normal equations)的方法

小小的总结–Gradient Descent Fro Linear Regression

• 当具体应用于线性回归的情况时，可以导出梯度下降方程的新形式。 我们可以替换我们的代价函数和我们的假设函数，并将方程修改为:

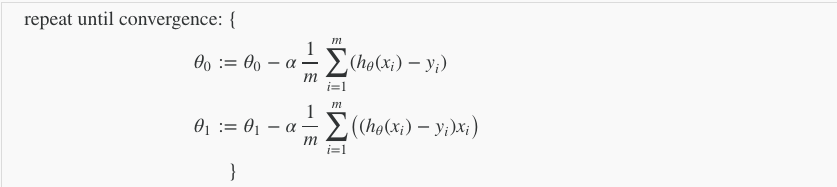
• 其中$m$是训练集的大小,$\theta_0$和$\theta_1$是同时更新的 $x_i,y_i$是给定训练集（数据）的值。
• 请注意，我们已将$\theta_j$分成$\theta_0$和$\theta_1$ 对于$\theta_1$来说,最后还有乘以一个$x_i$ 以下是对$\frac{\alpha}{\alpha\theta_j}J(\theta)$的推导:

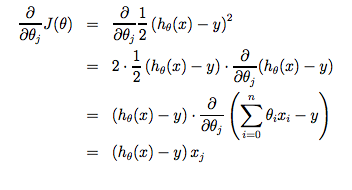
• 关键点是,我们从猜测假设函数开始,然后重复应用这些梯度下降方程，我们的假设将变得越来越准确。
• 因此，这只是原始代价函数J的梯度下降。该方法在每个步骤中用了整个训练集中的每个示例，并称为批量梯度下降。 需要注意的是，虽然梯度下降一般可以对局部最小值敏感，但我们在线性回归中提出的优化问题只有一个全局，而没有其他局部最优; 因此，梯度下降总是收敛（假设学习率α不是太大）到全局最小值。 实际上，J是凸二次函数。 下面是梯度下降的示例，因为它是为了最小化二次函数而运行的。

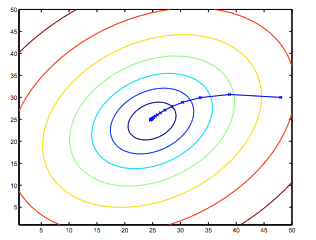
• 上面显示的椭圆是二次函数的轮廓。 还示出了梯度下降所采用的轨迹，其在（48,30）处初始化。 图中的x（由直线连接）标记了梯度下降经历的θ的连续值，当它收敛到其最小值时。